Lecture 4: Thermal Energy of Atoms and Molecules (part 1)
0) Orientation, admin, and quick recap
Welcome back! Just a quick administrative note: there's a problems class scheduled for this Friday. You can find the problem sheet already available on Blackboard. Roughly half of the problems on that sheet can be solved with the material we covered last week, and the rest will become accessible after we finish this week's lectures.
Today, we're going to continue our exploration of how atoms and molecules interact, building on the concepts of bond strength and equilibrium separation. We'll then pivot to understanding thermal energy and how it relates to temperature, particularly in gases. Last week, we discussed the interatomic potential well, characterising it with two key parameters: $a_0$, the equilibrium separation where attractive and repulsive forces balance, and $\varepsilon$, the separation or binding energy, which is the energy required to pull a pair of atoms infinitely far apart.
We established that the steep, short-range repulsion between atoms is primarily due to the Pauli exclusion principle, which prevents electron wavefunctions from overlapping. The attractive force we focused on last time was the van der Waals interaction, arising from induced dipoles. It's important to remember the scale of these forces: van der Waals bonds are relatively weak, typically in the milli-electron volt ($\text{meV}$) range, thousands of times weaker than strong bonds like ionic, covalent, or metallic bonds, which are in the electron volt ($\text{eV}$) range.
# 1) From latent heat to microscopic $\varepsilon$: nearest neighbours and double counting
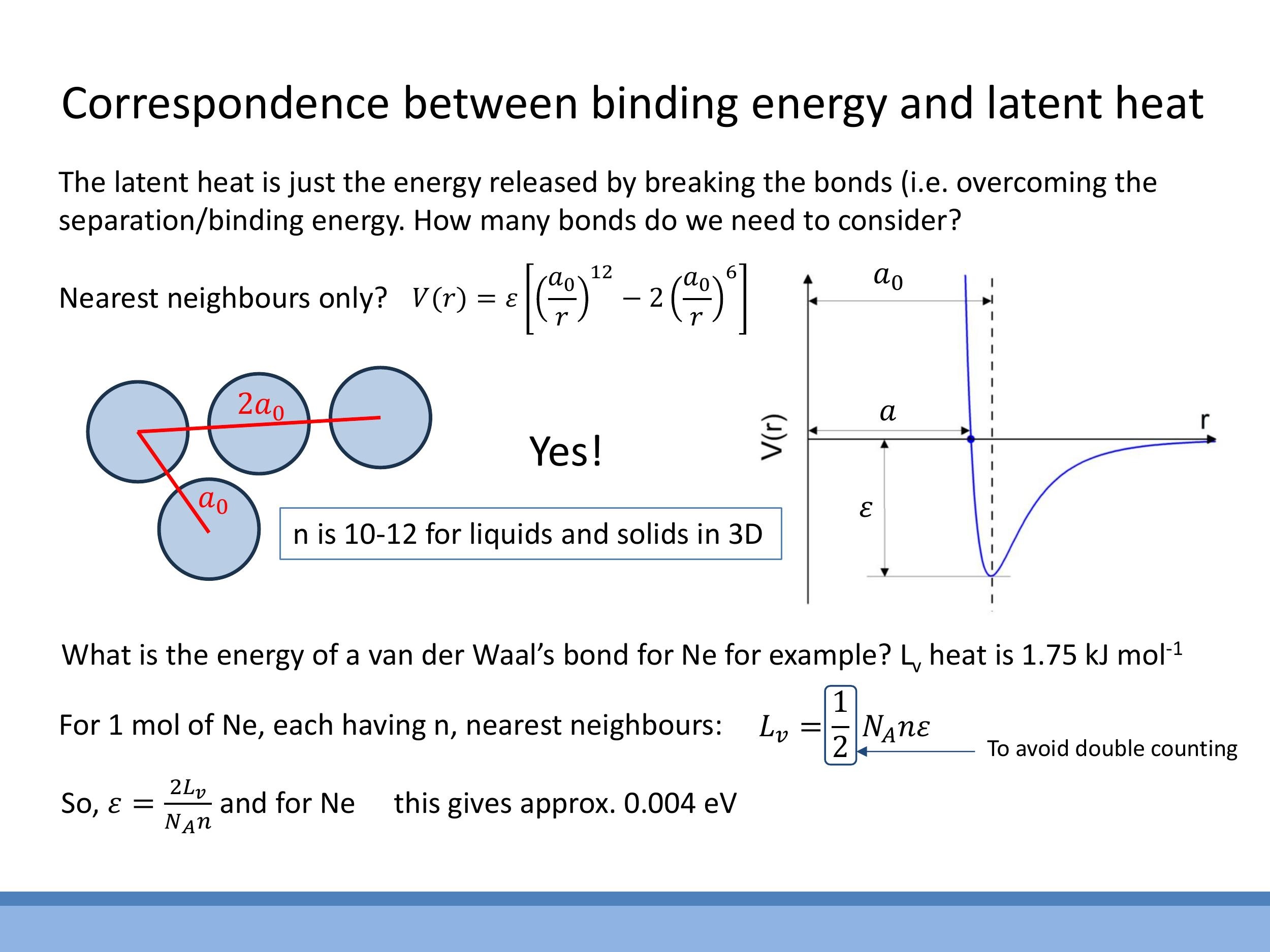
We can connect the macroscopic measurement of latent heat to the microscopic bond strength ($\varepsilon$). The latent heat of vaporisation, $L_v$, represents the total energy needed to break all intermolecular bonds in one mole of a substance, allowing it to transition from liquid to gas. For van der Waals systems, the potential energy $V(r)$ decays rapidly with distance, approximately as $r^{-6}$. This rapid decay means that interactions are dominated by an atom's nearest neighbours, allowing us to simplify our calculations by only considering these close contacts.
To relate the latent heat to the microscopic bond energy, we need to count the number of bonds. In liquids, a typical atom has about $n \approx 10$ nearest neighbours on average. For close-packed solids, this number is $n = 12$. However, when summing the energy, we must include a factor of $\frac{1}{2}$ to avoid double-counting, as each bond is shared between two atoms. Thus, the total latent heat of vaporisation can be expressed as:
$$
L_v = \frac{1}{2} N_A n \varepsilon
$$
where $N_A$ is Avogadro's number. This equation allows us to determine the microscopic separation energy $\varepsilon$ from a macroscopic measurement.
As a worked example, let's consider Neon. Given its latent heat of vaporisation $L_v = 1.75 \, \text{kJ mol}^{-1} $ and assuming $ n \approx 10 $ nearest neighbours (since it's a liquid at its boiling point), we can rearrange the formula to find $ \varepsilon$:
$$
\varepsilon = \frac{2 L_v}{N_A n}
$$
Plugging in the numbers, we obtain $\varepsilon \approx 0.004 \, \text{eV}$ per van der Waals bond. This calculation quantitatively confirms that van der Waals bonds are indeed thousands of times weaker than the electron-volt scale energies of strong chemical bonds.
⚠️ Exam Alert! The lecturer explicitly stated: "And this is not so different for a typical multiple choice question that you could get in the December multiple choice exam." You should be comfortable with this type of calculation, including the factor of $\frac{1}{2}$ for double-counting, and remembering typical nearest-neighbour counts ($n \approx 10$ for liquids, $n = 12$ for close-packed solids).
# 2) Three strong bond types: quick orientation
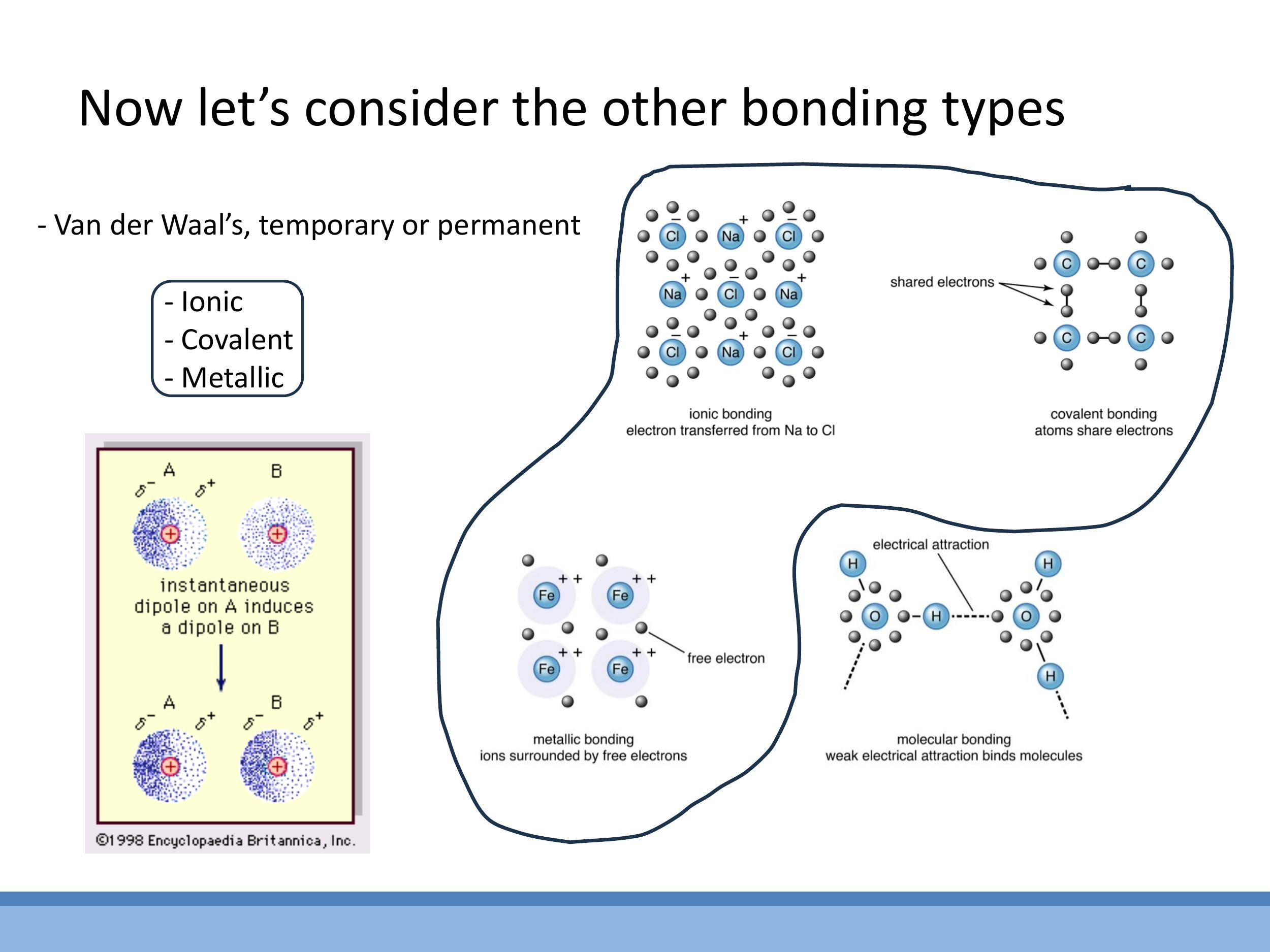
Beyond the weak van der Waals forces, there are three primary types of strong chemical bonds, all of which typically have strengths in the electron-volt ($\text{eV}$) range. These bonds are responsible for the robust structures of many materials.
Ionic bonds form when one atom effectively transfers one or more electrons to another, creating oppositely charged ions (cations and anions). The strong electrostatic Coulomb attraction between these ions then holds the material together. Covalent bonds involve the sharing of electron pairs between nuclei, creating a strong and often directional attraction. Finally, metallic bonds arise in metals where positive ion cores are embedded in a "sea" of delocalised valence electrons that are shared throughout the entire structure, leading to strong, non-directional bonding. Today, we'll delve into ionic bonding quantitatively, while covalent and metallic bonding will be discussed conceptually, focusing on their key characteristics.
# 3) Ionic bonding: long-range Coulomb attraction and lattice sums
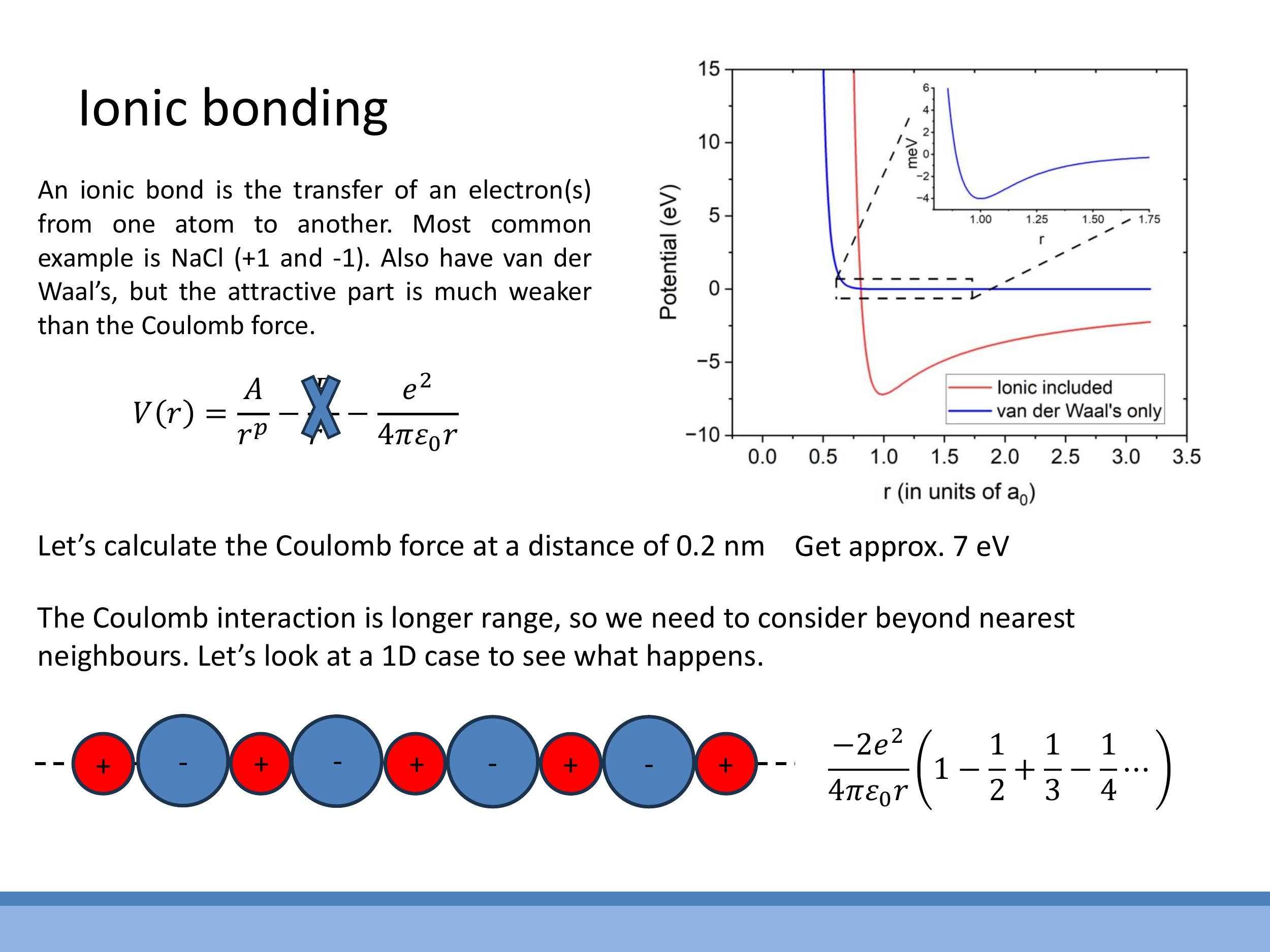
3.1 Potential model and a sense-check number
Ionic bonds are characterised by the transfer of electrons, leading to the formation of positive and negative ions. The dominant attractive force in these systems is the strong electrostatic Coulomb interaction between these oppositely charged ions. While van der Waals forces still exist, their contribution is negligible compared to the Coulomb force. We can model the potential energy $V(r)$ between two ions as the sum of a short-range repulsive term and a long-range Coulomb attractive term:
$$
V(r) = \frac{A}{r^p} - \frac{e^2}{4\pi\varepsilon_0 r}
$$
The second term represents the Coulomb attraction, where $e$ is the elementary charge and $\varepsilon_0$ is the permittivity of free space. To get a sense of the strength of this bond, if we calculate the Coulomb potential at a typical ionic separation of $r \approx 0.2 \, \text{nm} $ (or $ 2 \, \text{Å} $), we find it is approximately $ 7 \, \text{eV}$. This value firmly places ionic bonds in the "strong bond" category, significantly greater than van der Waals interactions.
3.2 Why nearest neighbours are not enough for ionic solids
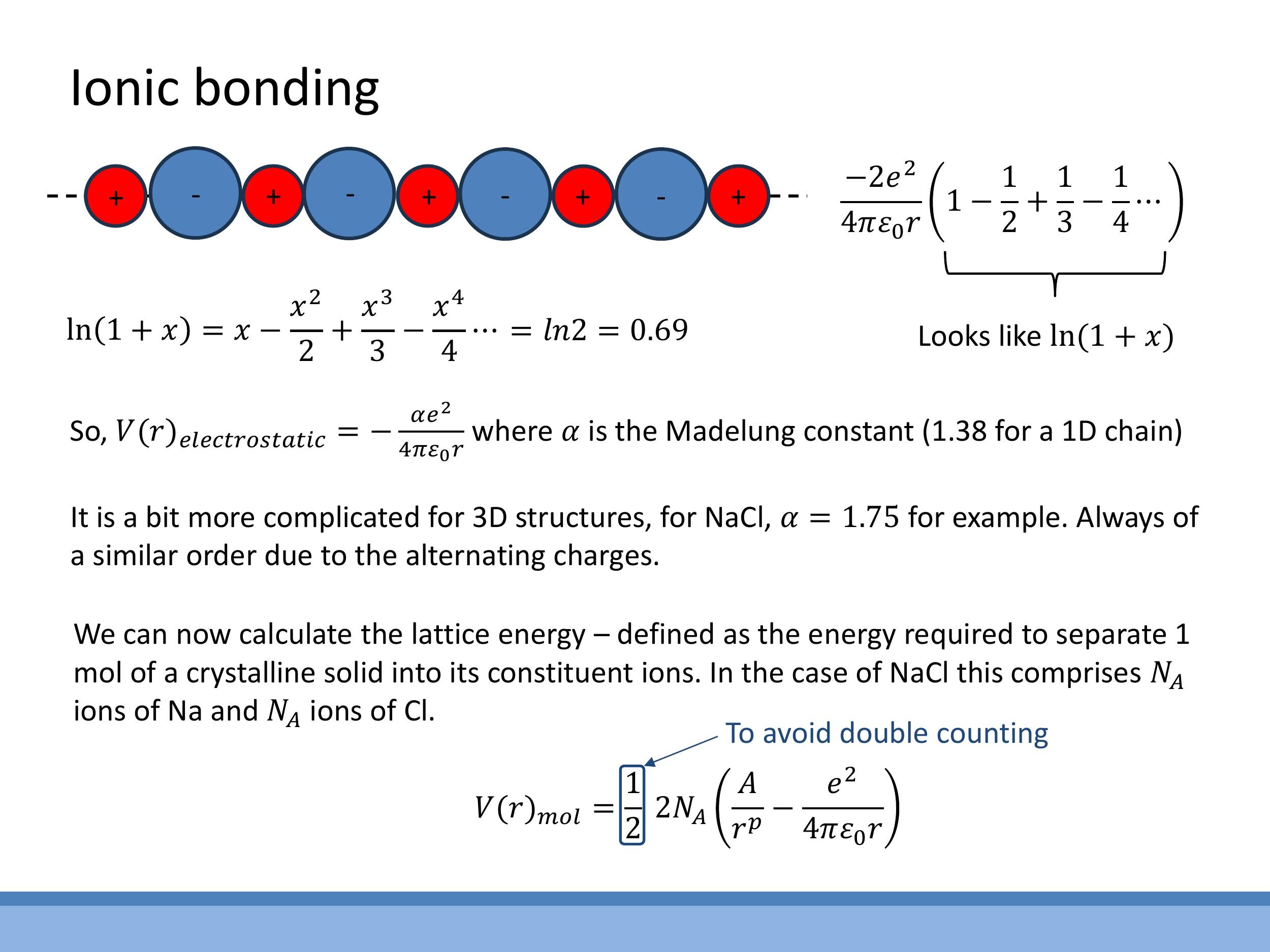
A crucial difference between ionic bonds and van der Waals bonds lies in the range of their attractive forces. The van der Waals potential decays rapidly (as $r^{-6}$), meaning only nearest neighbours contribute significantly. However, the Coulomb potential decays much more slowly, as $1/r$. This long-range nature implies that interactions with ions beyond just the nearest neighbours are significant and must be included in our calculations.
To illustrate this, consider a one-dimensional (1D) chain of alternating positive and negative ions. The total potential energy experienced by a single ion is the sum of interactions with all other ions in the chain. This leads to an alternating series: $1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \ldots$. This series converges to $\ln 2$. The numerical prefactor that arises from summing these long-range electrostatic interactions over the entire crystal lattice is called the Madelung constant, $\alpha$
$$
V_{\text{electrostatic}}(r) = -\frac{\alpha e^2}{4\pi\varepsilon_0 r}
$$
For a 1D chain, $\alpha \approx 1.38$. For more complex three-dimensional structures like sodium chloride (NaCl), $\alpha \approx 1.75$. In exam scenarios, you would typically be given the value of $\alpha$ and be expected to use it in calculations, rather than deriving it for complex 3D structures.
3.3 Lattice energy (definition and usage)
The lattice energy is defined as the energy required to completely separate one mole of a crystalline solid into its constituent gaseous ions. This is a macroscopic property that quantifies the overall strength of ionic bonding in a bulk material. For macroscopic crystals, the vast majority of atoms are in the interior, so contributions from ions at the edges or surfaces are negligible, and we typically only consider the bulk properties using the Madelung constant.
# 4) Covalent bonding: sharing electrons and the Morse potential
4.1 Mechanism and potential
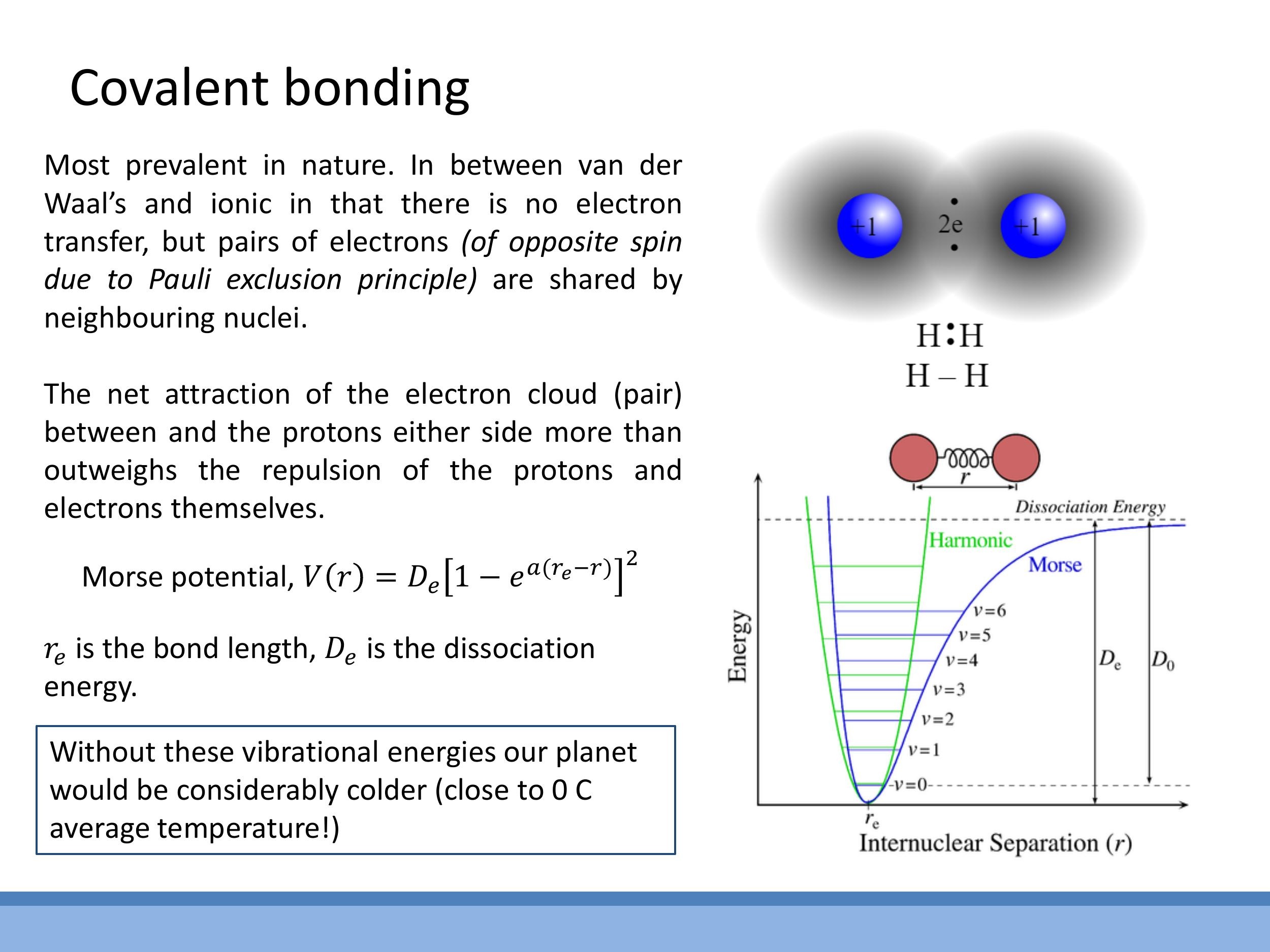
Covalent bonds are formed by the sharing of a pair of electrons, typically with opposite spins due to the Pauli exclusion principle, between two adjacent nuclei. This shared electron pair localises between the positive nuclei, creating a strong attractive force that overcomes the proton-proton repulsion and holds the atoms together. The strength of covalent bonds is comparable to that of ionic bonds.
The potential energy for a covalent bond is often described by the Morse potential:
$$
V(r) = D_e \left[ 1 - e^{a(r_e - r)} \right]^2
$$
Here, $r_e$ represents the equilibrium bond length, and $D_e$ is the dissociation energy, which is equivalent in meaning to the separation energy $\varepsilon$ we discussed earlier; it represents the depth of the potential well and the energy required to break the bond.
4.2 Vibrational levels and an Earth-system aside
Within the Morse potential well, molecules can occupy quantised vibrational energy states. These vibrational modes are crucial for understanding how atmospheric molecules like nitrogen ($N_2$) and carbon dioxide ($CO_2$) absorb infrared radiation. This absorption and subsequent re-emission of energy play a vital role in maintaining Earth's surface temperature, as these vibrating molecules contribute to the greenhouse effect.
4.3 Application: dissociation temperature for $H_2$
To illustrate the immense strength of covalent bonds, we can estimate the temperature required to dissociate a hydrogen molecule ($H_2$). We do this by equating the average thermal energy of a particle to the bond's dissociation energy. The average thermal energy for a particle in a gas is approximately $\frac{3}{2}kT$, where $k$ is Boltzmann's constant and $T$ is the absolute temperature. For $H_2$, the dissociation energy $D_e \approx 4.4 \, \text{eV}$.
Setting $\frac{3}{2}kT = D_e$, and solving for $T$:
$$
T = \frac{2 D_e}{3k}
$$
Using $D_e = 4.4 \, \text{eV} $ (and converting to Joules, $ 1 \, \text{eV} = 1.602 \times 10^{-19} \, \text{J} $), we find that $ T \approx 30,000 - 34,000 \, \text{K}$. This exceptionally high temperature highlights that covalent bonds are extremely strong on typical thermal scales, requiring enormous amounts of energy to break them.
⚠️ Exam Alert! The lecturer explicitly stated: "This is not so different from standard typical multiple choice questions that you'll get in December." You should be able to perform this type of calculation, converting between electron volts and Joules, and using Boltzmann's constant.

Metallic bonding is characterised by an array of positive ion cores immersed in a "sea" of delocalised valence electrons. These valence electrons are not bound to any single atom but are free to move throughout the entire metallic structure, forming a collective "electron gas" that holds the positive ions together. The strength of metallic bonds is generally comparable to that of ionic and covalent bonds, typically in the $\text{eV}$ range.
The strength of a metallic bond is influenced by the number of valence electrons contributed by each atom, which affects the density of the electron sea. For instance, Magnesium ($\text{Mg}$), with two valence electrons, forms stronger metallic bonds than Sodium ($\text{Na}$), which has only one. This difference in bond strength is reflected in their macroscopic properties, such as their latent heats of vaporisation: $\text{Mg}$ has a higher latent heat of vaporisation ($128 \, \text{kJ mol}^{-1} $) compared to $ \text{Na} $ ($ 97 \, \text{kJ mol}^{-1}$), indicating that more energy is required to break the bonds and vaporise Magnesium.
# 6) Thermal energy and the concept of temperature: starting kinetic theory of gases

Having explored interatomic bonds, we now transition to understanding thermal energy and the concept of temperature from the perspective of the kinetic theory of gases. This theory provides a microscopic foundation for macroscopic thermodynamic properties.
6.1 What makes a gas “ideal”
To simplify our analysis, we begin by considering an ideal gas, which is a theoretical model based on several key assumptions:
- The gas consists of a large number ($N$) of identical molecules, each with mass $m$.
- These molecules are treated as point particles, meaning their individual size is negligible compared to the average distance between them.
- All collisions, both between molecules and with the walls of the container, are perfectly elastic, conserving kinetic energy.
- The motion of the molecules is entirely random, with no preferred direction.
6.2 Pressure from molecular impacts: set-up and first steps
Pressure, a macroscopic property, arises from the force exerted by countless gas molecules colliding with the container walls. This force is a direct consequence of the change in momentum of the molecules as they rebound elastically from the walls.
Consider a single molecule of mass $m$ striking a wall perpendicularly with velocity $v_x$ and rebounding elastically. Its momentum changes from $mv_x$ to $-mv_x$, so the momentum transferred to the wall per collision is $2mv_x$. To calculate the total force, we need to determine how many molecules hit a given wall area $A$ in a certain time $t$. If we assume a uniform number density ($N/V$) and that, on average, half of the molecules are moving towards the wall, the number of collisions with wall area $A$ in time $t$ can be expressed as:
$$
\text{No. of collisions} = \frac{1}{2}\frac{N}{V} A v_x t
$$
This step establishes the rate at which momentum is transferred to the wall. The full derivation to obtain the pressure $P$ and link it directly to temperature will be completed in the next lecture.
# Slides present but not covered this lecture (for clarity)
Some slides pertaining to detailed Born-Landé lattice-energy derivation steps for NaCl and equilibrium conditions were present in the lecture material but were not covered in this session. This derivation will either appear in a later lecture or remains available for reference in the notes, but it was not taught in-session.
Key takeaways
- The well depth, $\varepsilon$, represents the microscopic "bond energy" or separation energy, while $a_0$ is the equilibrium spacing where the interatomic potential is at a minimum.
- For materials bonded by van der Waals forces, the latent heat of vaporisation ($L_v$) can be linked to $\varepsilon$ by considering nearest neighbours and applying a $\frac{1}{2}$ double-counting factor: $L_v = \frac{1}{2} N_A n \varepsilon$. Typical van der Waals $\varepsilon$ values range from $10^{-3}$ to $10^{-2} \, \text{eV}$.
- Strong bonds, including ionic, covalent, and metallic bonds, are significantly stronger, operating on the $\text{eV}$ scale. Ionic attraction is long-range ($1/r$), necessitating lattice sums that are captured by the Madelung constant, $\alpha$.
- Covalent bonds are effectively described by the Morse potential, where the dissociation energy $D_e$ is equivalent to $\varepsilon$. Dissociating an $H_2$ molecule, for example, requires temperatures around $3 \times 10^4 \, \text{K}$.
- Metallic bonding arises from a "sea" of delocalised electrons surrounding positive ion cores. Generally, a higher number of valence electrons contributes to strengthening the bond, as seen in the comparison between Magnesium ($\text{Mg}$) and Sodium ($\text{Na}$).
- The foundations of kinetic theory involve ideal gas assumptions, where pressure originates from the transfer of momentum during elastic collisions. We've established the initial step of counting collisions; the completion of the pressure-temperature relationship will be addressed in the next lecture.
## Lecture 4: Thermal Energy of Atoms and Molecules (part 1)
### 0) Orientation, admin, and quick recap
Welcome back! Just a quick administrative note: there's a problems class scheduled for this Friday. You can find the problem sheet already available on Blackboard. Roughly half of the problems on that sheet can be solved with the material we covered last week, and the rest will become accessible after we finish this week's lectures.
Today, we're going to continue our exploration of how atoms and molecules interact, building on the concepts of bond strength and equilibrium separation. We'll then pivot to understanding thermal energy and how it relates to temperature, particularly in gases. Last week, we discussed the interatomic potential well, characterising it with two key parameters: $a_0$, the equilibrium separation where attractive and repulsive forces balance, and $\varepsilon$, the separation or binding energy, which is the energy required to pull a pair of atoms infinitely far apart.
We established that the steep, short-range repulsion between atoms is primarily due to the Pauli exclusion principle, which prevents electron wavefunctions from overlapping. The attractive force we focused on last time was the van der Waals interaction, arising from induced dipoles. It's important to remember the scale of these forces: van der Waals bonds are relatively weak, typically in the milli-electron volt ($\text{meV}$) range, thousands of times weaker than strong bonds like ionic, covalent, or metallic bonds, which are in the electron volt ($\text{eV}$) range.
## # 1) From latent heat to microscopic $\varepsilon$: nearest neighbours and double counting

We can connect the macroscopic measurement of latent heat to the microscopic bond strength ($\varepsilon$). The latent heat of vaporisation, $L_v$, represents the total energy needed to break all intermolecular bonds in one mole of a substance, allowing it to transition from liquid to gas. For van der Waals systems, the potential energy $V(r)$ decays rapidly with distance, approximately as $r^{-6}$. This rapid decay means that interactions are dominated by an atom's nearest neighbours, allowing us to simplify our calculations by only considering these close contacts.
To relate the latent heat to the microscopic bond energy, we need to count the number of bonds. In liquids, a typical atom has about $n \approx 10$ nearest neighbours on average. For close-packed solids, this number is $n = 12$. However, when summing the energy, we must include a factor of $\frac{1}{2}$ to avoid double-counting, as each bond is shared between two atoms. Thus, the total latent heat of vaporisation can be expressed as:
$$ L_v = \frac{1}{2} N_A n \varepsilon $$
where $N_A$ is Avogadro's number. This equation allows us to determine the microscopic separation energy $\varepsilon$ from a macroscopic measurement.
As a worked example, let's consider Neon. Given its latent heat of vaporisation $L_v = 1.75\,\text{kJ mol}^{-1}$ and assuming $n \approx 10$ nearest neighbours (since it's a liquid at its boiling point), we can rearrange the formula to find $\varepsilon$:
$$ \varepsilon = \frac{2 L_v}{N_A n} $$
Plugging in the numbers, we obtain $\varepsilon \approx 0.004\,\text{eV}$ per van der Waals bond. This calculation quantitatively confirms that van der Waals bonds are indeed thousands of times weaker than the electron-volt scale energies of strong chemical bonds.
> **⚠️ Exam Alert!** The lecturer explicitly stated: "And this is not so different for a typical multiple choice question that you could get in the December multiple choice exam." You should be comfortable with this type of calculation, including the factor of $\frac{1}{2}$ for double-counting, and remembering typical nearest-neighbour counts ($n \approx 10$ for liquids, $n = 12$ for close-packed solids).
## # 2) Three strong bond types: quick orientation

Beyond the weak van der Waals forces, there are three primary types of strong chemical bonds, all of which typically have strengths in the electron-volt ($\text{eV}$) range. These bonds are responsible for the robust structures of many materials.
**Ionic bonds** form when one atom effectively transfers one or more electrons to another, creating oppositely charged ions (cations and anions). The strong electrostatic Coulomb attraction between these ions then holds the material together. **Covalent bonds** involve the sharing of electron pairs between nuclei, creating a strong and often directional attraction. Finally, **metallic bonds** arise in metals where positive ion cores are embedded in a "sea" of delocalised valence electrons that are shared throughout the entire structure, leading to strong, non-directional bonding. Today, we'll delve into ionic bonding quantitatively, while covalent and metallic bonding will be discussed conceptually, focusing on their key characteristics.
## # 3) Ionic bonding: long-range Coulomb attraction and lattice sums

#### 3.1 Potential model and a sense-check number
Ionic bonds are characterised by the transfer of electrons, leading to the formation of positive and negative ions. The dominant attractive force in these systems is the strong electrostatic Coulomb interaction between these oppositely charged ions. While van der Waals forces still exist, their contribution is negligible compared to the Coulomb force. We can model the potential energy $V(r)$ between two ions as the sum of a short-range repulsive term and a long-range Coulomb attractive term:
$$ V(r) = \frac{A}{r^p} - \frac{e^2}{4\pi\varepsilon_0 r} $$
The second term represents the Coulomb attraction, where $e$ is the elementary charge and $\varepsilon_0$ is the permittivity of free space. To get a sense of the strength of this bond, if we calculate the Coulomb potential at a typical ionic separation of $r \approx 0.2\,\text{nm}$ (or $2\,\text{Å}$), we find it is approximately $7\,\text{eV}$. This value firmly places ionic bonds in the "strong bond" category, significantly greater than van der Waals interactions.
#### 3.2 Why nearest neighbours are not enough for ionic solids

A crucial difference between ionic bonds and van der Waals bonds lies in the range of their attractive forces. The van der Waals potential decays rapidly (as $r^{-6}$), meaning only nearest neighbours contribute significantly. However, the Coulomb potential decays much more slowly, as $1/r$. This long-range nature implies that interactions with ions beyond just the nearest neighbours are significant and must be included in our calculations.
To illustrate this, consider a one-dimensional (1D) chain of alternating positive and negative ions. The total potential energy experienced by a single ion is the sum of interactions with all other ions in the chain. This leads to an alternating series: $1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \ldots$. This series converges to $\ln 2$. The numerical prefactor that arises from summing these long-range electrostatic interactions over the entire crystal lattice is called the **Madelung constant, $\alpha$**. The electrostatic potential for an ion in a lattice can then be expressed as:
$$ V_{\text{electrostatic}}(r) = -\frac{\alpha e^2}{4\pi\varepsilon_0 r} $$
For a 1D chain, $\alpha \approx 1.38$. For more complex three-dimensional structures like sodium chloride (NaCl), $\alpha \approx 1.75$. In exam scenarios, you would typically be given the value of $\alpha$ and be expected to use it in calculations, rather than deriving it for complex 3D structures.
#### 3.3 Lattice energy (definition and usage)
The **lattice energy** is defined as the energy required to completely separate one mole of a crystalline solid into its constituent gaseous ions. This is a macroscopic property that quantifies the overall strength of ionic bonding in a bulk material. For macroscopic crystals, the vast majority of atoms are in the interior, so contributions from ions at the edges or surfaces are negligible, and we typically only consider the bulk properties using the Madelung constant.
## # 4) Covalent bonding: sharing electrons and the Morse potential

#### 4.1 Mechanism and potential
Covalent bonds are formed by the sharing of a pair of electrons, typically with opposite spins due to the Pauli exclusion principle, between two adjacent nuclei. This shared electron pair localises between the positive nuclei, creating a strong attractive force that overcomes the proton-proton repulsion and holds the atoms together. The strength of covalent bonds is comparable to that of ionic bonds.
The potential energy for a covalent bond is often described by the **Morse potential**:
$$ V(r) = D_e \left[ 1 - e^{a(r_e - r)} \right]^2 $$
Here, $r_e$ represents the equilibrium bond length, and $D_e$ is the **dissociation energy**, which is equivalent in meaning to the separation energy $\varepsilon$ we discussed earlier; it represents the depth of the potential well and the energy required to break the bond.
#### 4.2 Vibrational levels and an Earth-system aside
Within the Morse potential well, molecules can occupy quantised vibrational energy states. These vibrational modes are crucial for understanding how atmospheric molecules like nitrogen ($N_2$) and carbon dioxide ($CO_2$) absorb infrared radiation. This absorption and subsequent re-emission of energy play a vital role in maintaining Earth's surface temperature, as these vibrating molecules contribute to the greenhouse effect.
#### 4.3 Application: dissociation temperature for $H_2$
To illustrate the immense strength of covalent bonds, we can estimate the temperature required to dissociate a hydrogen molecule ($H_2$). We do this by equating the average thermal energy of a particle to the bond's dissociation energy. The average thermal energy for a particle in a gas is approximately $\frac{3}{2}kT$, where $k$ is Boltzmann's constant and $T$ is the absolute temperature. For $H_2$, the dissociation energy $D_e \approx 4.4\,\text{eV}$.
Setting $\frac{3}{2}kT = D_e$, and solving for $T$:
$$ T = \frac{2 D_e}{3k} $$
Using $D_e = 4.4\,\text{eV}$ (and converting to Joules, $1\,\text{eV} = 1.602 \times 10^{-19}\,\text{J}$), we find that $T \approx 30,000 - 34,000\,\text{K}$. This exceptionally high temperature highlights that covalent bonds are extremely strong on typical thermal scales, requiring enormous amounts of energy to break them.
> **⚠️ Exam Alert!** The lecturer explicitly stated: "This is not so different from standard typical multiple choice questions that you'll get in December." You should be able to perform this type of calculation, converting between electron volts and Joules, and using Boltzmann's constant.
## # 5) Metallic bonding: electron sea and trends

Metallic bonding is characterised by an array of positive ion cores immersed in a "sea" of delocalised valence electrons. These valence electrons are not bound to any single atom but are free to move throughout the entire metallic structure, forming a collective "electron gas" that holds the positive ions together. The strength of metallic bonds is generally comparable to that of ionic and covalent bonds, typically in the $\text{eV}$ range.
The strength of a metallic bond is influenced by the number of valence electrons contributed by each atom, which affects the density of the electron sea. For instance, Magnesium ($\text{Mg}$), with two valence electrons, forms stronger metallic bonds than Sodium ($\text{Na}$), which has only one. This difference in bond strength is reflected in their macroscopic properties, such as their latent heats of vaporisation: $\text{Mg}$ has a higher latent heat of vaporisation ($128\,\text{kJ mol}^{-1}$) compared to $\text{Na}$ ($97\,\text{kJ mol}^{-1}$), indicating that more energy is required to break the bonds and vaporise Magnesium.
## # 6) Thermal energy and the concept of temperature: starting kinetic theory of gases

Having explored interatomic bonds, we now transition to understanding thermal energy and the concept of temperature from the perspective of the kinetic theory of gases. This theory provides a microscopic foundation for macroscopic thermodynamic properties.
#### 6.1 What makes a gas “ideal”
To simplify our analysis, we begin by considering an ideal gas, which is a theoretical model based on several key assumptions:
1. The gas consists of a large number ($N$) of identical molecules, each with mass $m$.
2. These molecules are treated as point particles, meaning their individual size is negligible compared to the average distance between them.
3. All collisions, both between molecules and with the walls of the container, are perfectly elastic, conserving kinetic energy.
4. The motion of the molecules is entirely random, with no preferred direction.
#### 6.2 Pressure from molecular impacts: set-up and first steps
Pressure, a macroscopic property, arises from the force exerted by countless gas molecules colliding with the container walls. This force is a direct consequence of the change in momentum of the molecules as they rebound elastically from the walls.
Consider a single molecule of mass $m$ striking a wall perpendicularly with velocity $v_x$ and rebounding elastically. Its momentum changes from $mv_x$ to $-mv_x$, so the momentum transferred to the wall per collision is $2mv_x$. To calculate the total force, we need to determine how many molecules hit a given wall area $A$ in a certain time $t$. If we assume a uniform number density ($N/V$) and that, on average, half of the molecules are moving towards the wall, the number of collisions with wall area $A$ in time $t$ can be expressed as:
$$ \text{No. of collisions} = \frac{1}{2}\frac{N}{V} A v_x t $$
This step establishes the rate at which momentum is transferred to the wall. The full derivation to obtain the pressure $P$ and link it directly to temperature will be completed in the next lecture.
## # Slides present but not covered this lecture (for clarity)
Some slides pertaining to detailed Born-Landé lattice-energy derivation steps for NaCl and equilibrium conditions were present in the lecture material but were not covered in this session. This derivation will either appear in a later lecture or remains available for reference in the notes, but it was not taught in-session.
## Key takeaways
* The well depth, $\varepsilon$, represents the microscopic "bond energy" or separation energy, while $a_0$ is the equilibrium spacing where the interatomic potential is at a minimum.
* For materials bonded by van der Waals forces, the latent heat of vaporisation ($L_v$) can be linked to $\varepsilon$ by considering nearest neighbours and applying a $\frac{1}{2}$ double-counting factor: $L_v = \frac{1}{2} N_A n \varepsilon$. Typical van der Waals $\varepsilon$ values range from $10^{-3}$ to $10^{-2}\,\text{eV}$.
* Strong bonds, including ionic, covalent, and metallic bonds, are significantly stronger, operating on the $\text{eV}$ scale. Ionic attraction is long-range ($1/r$), necessitating lattice sums that are captured by the Madelung constant, $\alpha$.
* Covalent bonds are effectively described by the Morse potential, where the dissociation energy $D_e$ is equivalent to $\varepsilon$. Dissociating an $H_2$ molecule, for example, requires temperatures around $3 \times 10^4\,\text{K}$.
* Metallic bonding arises from a "sea" of delocalised electrons surrounding positive ion cores. Generally, a higher number of valence electrons contributes to strengthening the bond, as seen in the comparison between Magnesium ($\text{Mg}$) and Sodium ($\text{Na}$).
* The foundations of kinetic theory involve ideal gas assumptions, where pressure originates from the transfer of momentum during elastic collisions. We've established the initial step of counting collisions; the completion of the pressure-temperature relationship will be addressed in the next lecture.






