Lecture 15: Elastic Solids - from stress-strain to atoms-on-springs
0) Orientation, admin, and bridge from crystals
This lecture marks the conclusion of new material for the Properties of Matter course. Following this, the problems class scheduled for Friday is cancelled. It will be replaced by a two-hour revision session covering both Mechanics and Properties of Matter. During this session, the lecturer will highlight key slides and topics that are particularly important for the upcoming exam.
This lecture bridges from the previous discussion on crystalline structures and atomic packing to exploring how solids deform under external loads. The objective is to establish a link between macroscopic elastic behaviour, such as stress-strain relationships and Young's modulus, and the underlying microscopic interatomic forces. The lecture concludes by examining entropy-driven elasticity in materials like rubber.
1) How solids respond to loads: types of stress and deformation
Materials respond to external forces, or loads, through various forms of deformation. Stress is defined as the load applied per unit area, and the resulting deformation depends on how this load is distributed.
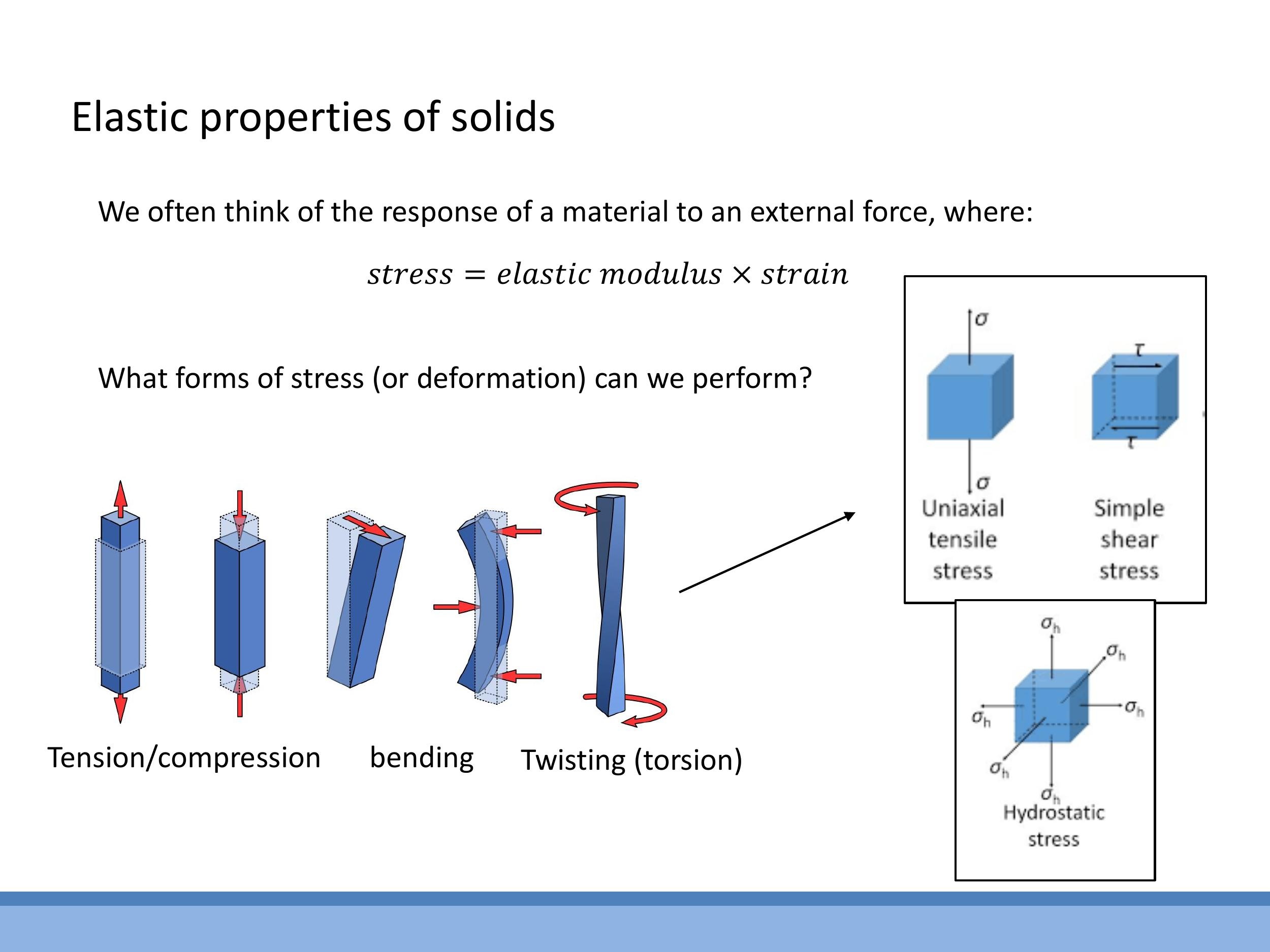
Common types of loading and their corresponding deformations include:
- Tension/Compression (Uniaxial): A force applied along a single axis, causing the material to stretch (tension) or squash (compression).
- Bending: A load applied transversely, causing the material to curve. An example is the three-point bend setup, which students encountered in a formative laboratory experiment.
- Twisting (Torsion): A torque applied about an axis, causing the material to twist.
- Hydrostatic Stress: Uniform compression applied from all directions, often encountered in high-pressure environments, such as within high-pressure cells.
2) Stress, strain, and Young’s modulus: the linear elastic regime
In the context of tensile loading, two fundamental quantities define a material's mechanical response:
- Tensile Stress ($\sigma$): Defined as the force ($F$) applied per unit cross-sectional area ($A$).
$$ \sigma = \frac{F}{A} $$
- Tensile Strain ($\varepsilon$): Defined as the fractional change in length ($\Delta l$) relative to the original length ($l$).
$$ \varepsilon = \frac{\Delta l}{l} $$

Young's Modulus ($E$), also known as the modulus of elasticity, quantifies a material's stiffness in the initial linear elastic region of its stress-strain curve. It is the ratio of tensile stress to tensile strain:
$$
E = \frac{\sigma}{\varepsilon} = \frac{F/A}{\Delta l/l}
$$
This equation can be rearranged to express the force required for a given extension:
$$
F = \left( \frac{AE}{l} \right) \Delta l
$$
This form is analogous to Hooke's law, $F = kx$, where the term $\left( \frac{AE}{l} \right)$ represents an effective spring constant $k_{\text{eff}}$ for the material bar. This implies that within the elastic regime, a solid bar under tension behaves similarly to an ideal spring, with its "springiness" determined by its cross-sectional area ($A$), Young's modulus ($E$), and length ($l$).
3) Reading a stress-strain curve: elastic limit, yield, hardening, necking, fracture
The stress-strain curve provides a comprehensive overview of a material's mechanical behaviour under increasing load.
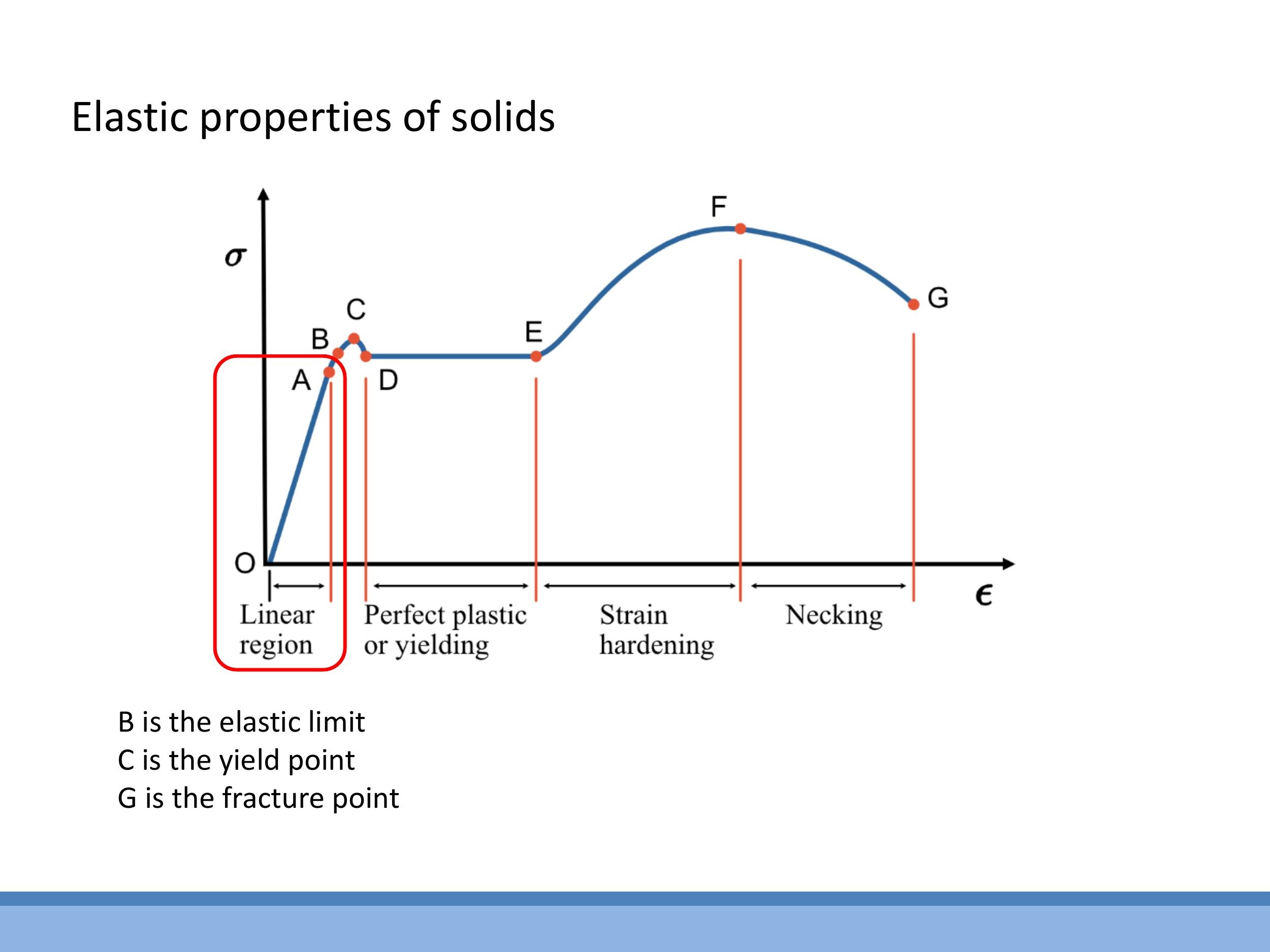
Starting from the origin ($O$), the curve typically exhibits several distinct regions:
- Linear Elastic Region (O to B): In this initial segment, stress is directly proportional to strain, and the material returns to its original dimensions upon removal of the load. The slope of this linear portion is defined as Young's Modulus ($E$).
- Elastic Limit (B) and Yield Point (C): Beyond point B, the material starts to undergo permanent, or plastic, deformation. Point C, the yield point, specifically marks the onset of this irreversible deformation.
- Plastic Deformation: In this regime, the material's internal structure changes permanently. At a microscopic level, this involves the movement of defects called dislocations within the crystal lattice, leading to the irreversible slipping of atomic planes past one another.
- Strain (Work) Hardening (towards F): As plastic deformation continues, the material can become stiffer and harder. This occurs because the movement and accumulation of dislocations impede further slip, increasing the material's resistance to deformation. A common example is bending a copper wire, which becomes harder and more brittle if re-bent due to this work hardening.
- Necking and Fracture (F to G): In the final stages of tensile loading, the material begins to thin locally, a phenomenon known as necking. This localized reduction in cross-sectional area leads to a rapid increase in true stress until the material ultimately fractures at point G.
4) Quantitative elasticity: extensions and stored energy
4.1 Extensions under load: order-of-magnitude checks
The relationship $F = \left( \frac{AE}{l} \right) \Delta l$ can be rearranged to calculate the extension $\Delta l = \frac{Fl}{AE}$. This formula is crucial for estimating deformations under various loads. For instance, a $4.5 \, \text{m} $ copper wire with a diameter of $ 120 \, \mu\text{m} $ subjected to loads between $ 50 \, \text{g} $ and $ 150 \, \text{g} $ will experience elastic extensions on the order of $ 1 \, \text{mm} $ per added load. Similarly, a $ 1500 \, \text{kg} $ car suspended on a $ 2 \, \text{m} $ steel cable with a $ 10 \, \text{mm} $ diameter (where $ E \approx 200 \, \text{GPa} $) would cause the cable to extend by approximately $ 2 \, \text{mm}$. These calculations highlight that extensions in metre-scale metallic structures under typical loads are often in the millimetre range, which is useful for performing back-of-the-envelope checks to assess the physical reasonableness of results.
⚠️ Exam Alert! The lecturer explicitly stated: "This is not so different to the kind of questions you get in the multiple choice exam. In fact, this resembles one from last year, I think." Students should be prepared for calculations involving the extension of materials like steel cables supporting vehicles.
4.2 Energy stored in elastic extension
When a material is stretched within its elastic limit, work is done against the interatomic forces, and this energy is stored as elastic potential energy in the stretched bonds. The work ($W$) done in extending a material from zero to an extension $\Delta l$ can be derived by integrating the force over the displacement:
$$
W = \int F \, d(\Delta l)
$$
Substituting $F = \left( \frac{AE}{l} \right) \Delta l$, the integral becomes:
$$
W = \int_0^{\Delta l} \left( \frac{AE}{l} \right) \Delta l' \, d(\Delta l') = \frac{AE}{l} \left[ \frac{(\Delta l')^2}{2} \right]_0^{\Delta l} = \frac{AE}{2l} (\Delta l)^2
$$
This stored elastic energy, for the car-cable example, amounts to approximately $23 \, \text{J}$.
⚠️ Exam Alert! The lecturer explicitly stated: "This sort of question is precisely what appeared in last year's multiple choice exam." Students should be proficient in computing stored elastic energy given the extension and material dimensions.
4.3 Live demo narrative: spotting the yield point with a copper wire
A live demonstration involving a long copper wire suspended with a ruler illustrates the transition from elastic to plastic deformation. Initially, the addition of $50 \, \text{g} $ weights causes visible elastic extensions, typically around $ 1.5 \, \text{mm} $ to $ 2 \, \text{mm} $ per weight. Up to a total load of approximately $ 150 \, \text{g} $ to $ 200 \, \text{g}$, the wire stretches reversibly. However, beyond this point, the wire begins to stretch continuously and rapidly, indicating that the yield strength has been exceeded and plastic deformation has commenced. Upon removal of the loads, the wire does not return to its original baseline length, confirming permanent deformation.
The yield strength for copper is typically in the order of tens of megapascals ($\text{MPa}$). Using the relationship $\sigma_y \approx F_y/A$, one can estimate the maximum "safe" load ($F_y$) that a wire of a given cross-sectional area ($A$) can withstand before yielding. Microscopically, in the elastic region, atomic bonds stretch reversibly. Beyond the yield point, dislocations move and atomic planes slip, leading to permanent set and potentially subsequent strain hardening.
5) From atoms to E: deriving Young’s modulus from the interatomic potential
The macroscopic elastic properties of a solid can be derived from its fundamental interatomic potential. This approach re-establishes the "atoms-on-springs" model.
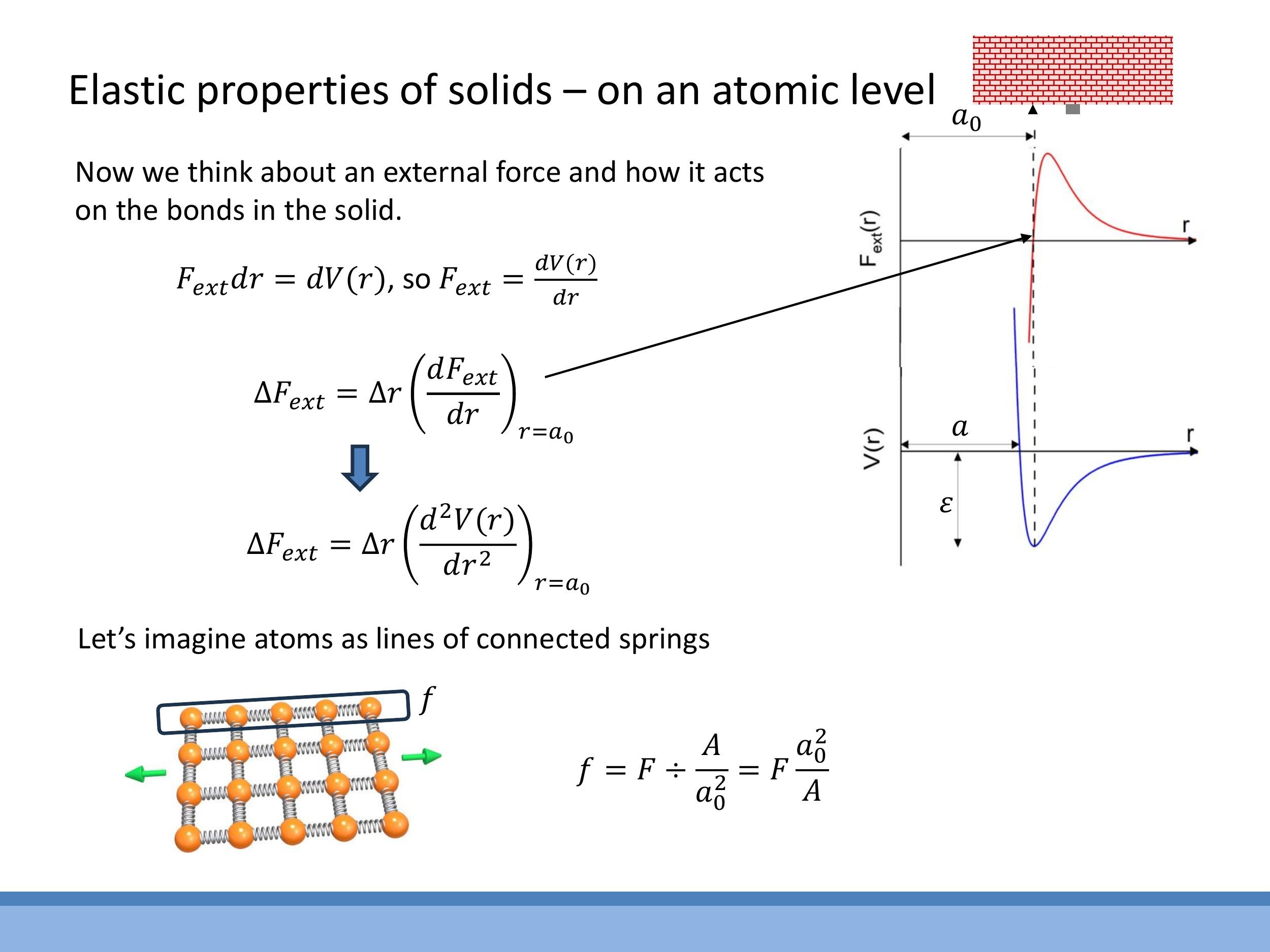

The interatomic potential $V(r)$ describes the energy of interaction between two atoms as a function of their separation $r$. Key features of this potential include:
- An equilibrium separation $a_0$, corresponding to the minimum of the potential well, where the net force between atoms is zero.
- A well depth $\varepsilon$, representing the bond or separation energy required to fully separate the atoms.
The interatomic force $F$ is related to the potential by $F = dV/dr$. For small displacements $\Delta r$ around the equilibrium separation $a_0$, the change in force $\Delta F$ can be approximated linearly:
$$ \Delta F \approx \Delta r \left( \frac{dF}{dr} \right) {r=a_0} = \Delta r \left( \frac{d^2V}{dr^2} \right) {r=a_0} $$
This expression $\left( \frac{d^2V}{dr^2} \right)_{r=a_0}$ represents the "stiffness" of a single bond, analogous to a spring constant.
To bridge the microscopic and macroscopic scales, the following relationships are used:
- The force per bond ($f$) is related to the macroscopic force ($F$) and cross-sectional area ($A$) by considering the density of bonds across that area: $f = F \left( \frac{a_0^2}{A} \right)$.
- The macroscopic extension ($\Delta l$) is related to the bond extension ($\Delta r$) by considering the number of bonds in series along the length ($l$): $\Delta l = \Delta r \left( \frac{l}{a_0} \right)$.
Substituting these microscopic expressions into the definition of Young's Modulus $E = (F/A) / (\Delta l/l)$ yields:
$$ E = \frac{1}{a_0} \left( \frac{d^2V}{dr^2} \right)_{r=a_0} $$
This fundamental equation relates the macroscopic Young's Modulus directly to the curvature of the interatomic potential at the equilibrium separation.
For a worked example, consider solid argon, which can be modelled by a Lennard-Jones potential. For this potential, the second derivative at equilibrium is $\left( \frac{d^2V}{dr^2} \right)_{r=a_0} = \frac{72\varepsilon}{a_0^2}$. Substituting this into the derived equation for $E$ gives $E = \frac{72\varepsilon}{a_0^3}$. Using typical values for argon ($a_0 \approx 3.7 \times 10^{-10} \, \text{m} $ and $ \varepsilon \approx 1.7 \times 10^{-21} \, \text{J} $), the calculated Young's modulus is approximately $ 2.4 \, \text{GPa} $. This value is about a factor of two smaller than the measured value of $ 4.8 \, \text{GPa}$. The discrepancy arises because this simplified "independent chains" model neglects the lateral coupling and interactions between neighbouring rows of atoms, which contribute to the overall stiffness. Despite this, it provides a remarkably accurate order-of-magnitude estimate from first principles.
6) Entropic elasticity: why rubber heats when stretched and contracts when heated
Rubber, a polymer, exhibits a unique form of elasticity driven primarily by entropy rather than direct bond stretching. At a microscopic level, rubber consists of long polymer chains that naturally prefer a tangled, disordered state, which corresponds to a high-entropy configuration. When a rubber band is stretched, these chains are forced to align, resulting in a more ordered, lower-entropy state.
This entropic effect explains the observed elastocaloric phenomena:
- Stretching and Heating: When a rubber band is stretched rapidly, its internal entropy decreases. For the total entropy of the universe to uphold the Second Law of Thermodynamics (i.e., $\Delta S_{\text{universe}} \geq 0$), the system must expel heat to its surroundings. This expelled heat is perceived as warmth. If the stretched band is held, it gradually cools back to ambient temperature as it exchanges heat with the surroundings.
- Relaxation and Cooling: Conversely, when a stretched rubber band is quickly released, the polymer chains spontaneously return to their high-entropy, tangled state. This increase in the system's entropy leads to the absorption of heat from the surroundings, causing the band to feel cool.
- Heating a Hanging Band: Unlike metals, which expand and lengthen when heated due to increased atomic vibrations, a hanging rubber band contracts when heated. The added thermal energy increases the number of accessible microstates for the polymer chains, driving them to "recrumple" towards a state of higher entropy. This entropic drive causes the band to shorten and lift any attached weight, a phenomenon that can be visibly demonstrated with a heat gun.
7) Consolidation and next steps
This course has explored the mechanical properties of materials, bridging macroscopic observations with microscopic models.
- Macroscopic and Quantitative Tools: We defined stress ($\sigma = F/A$), strain ($\varepsilon = \Delta l/l$), and Young's modulus ($E = \sigma/\varepsilon$). We analysed the stress-strain curve, identifying regions of linear elasticity, yield, plastic deformation, strain hardening, necking, and fracture. Quantitative tools derived include the extension of a bar under load ($\Delta l = Fl/(AE)$) and the elastic energy stored within it ($W = (AE/2l) (\Delta l)^2$), allowing for order-of-magnitude estimates that are typically in the millimetre range for metre-scale metals.
- Microscopic Models and Thermodynamics: We linked Young's modulus to the curvature of the interatomic potential at equilibrium ($E = (1/a_0) (d^2V/dr^2)|_{r=a_0}$), demonstrating that the "atoms-as-springs" model provides a powerful first-principles understanding of material stiffness. Furthermore, the concept of entropic elasticity was used to explain the unique behaviour of rubber, specifically its heating upon stretching and contraction upon heating, in terms of changes in polymer chain disorder and the Second Law of Thermodynamics.
This concludes the new material for the course. A two-hour revision session, covering both Mechanics and Properties of Matter, will replace the cancelled problems class next week. The lecturer will highlight key slides and topics relevant for the upcoming exam during this session.
Key takeaways
- Stress-strain: $\sigma = F/A$, $\varepsilon = \Delta l/l$. In the elastic region, $\sigma \propto \varepsilon$ with slope $E$; beyond the yield point, plastic deformation sets in via dislocation motion, followed by strain hardening, necking, and fracture.
- A bar in tension behaves like a spring with an effective spring constant $k_{\text{eff}} = AE/l$; extensions $\Delta l = Fl/(AE)$ are typically millimetres for metre-scale metals under practical loads.
- Elastic energy stored by stretching is $W = (AE/2l) (\Delta l)^2$.
- Microscopic origin of stiffness: $E = (1/a_0) (d^2V/dr^2)|_{r=a_0}$. For Lennard-Jones solids (e.g., Ar), this provides the correct order of magnitude; discrepancies are explained by neglecting neighbour coupling.
- Rubber’s elasticity is entropic: stretching lowers the polymer chains' entropy and causes heat expulsion; heating increases entropy and results in contraction under load.
- Administrative: this is the final new-content lecture; a two-hour revision session (covering Mechanics + Properties of Matter) replaces the cancelled problems class and will highlight likely exam-relevant material.
## Lecture 15: Elastic Solids - from stress-strain to atoms-on-springs
### 0) Orientation, admin, and bridge from crystals
This lecture marks the conclusion of new material for the Properties of Matter course. Following this, the problems class scheduled for Friday is cancelled. It will be replaced by a two-hour revision session covering both Mechanics and Properties of Matter. During this session, the lecturer will highlight key slides and topics that are particularly important for the upcoming exam.
This lecture bridges from the previous discussion on crystalline structures and atomic packing to exploring how solids deform under external loads. The objective is to establish a link between macroscopic elastic behaviour, such as stress-strain relationships and Young's modulus, and the underlying microscopic interatomic forces. The lecture concludes by examining entropy-driven elasticity in materials like rubber.
### 1) How solids respond to loads: types of stress and deformation
Materials respond to external forces, or loads, through various forms of deformation. Stress is defined as the load applied per unit area, and the resulting deformation depends on how this load is distributed.

Common types of loading and their corresponding deformations include:
* **Tension/Compression (Uniaxial):** A force applied along a single axis, causing the material to stretch (tension) or squash (compression).
* **Bending:** A load applied transversely, causing the material to curve. An example is the three-point bend setup, which students encountered in a formative laboratory experiment.
* **Twisting (Torsion):** A torque applied about an axis, causing the material to twist.
* **Hydrostatic Stress:** Uniform compression applied from all directions, often encountered in high-pressure environments, such as within high-pressure cells.
### 2) Stress, strain, and Young’s modulus: the linear elastic regime
In the context of tensile loading, two fundamental quantities define a material's mechanical response:
* **Tensile Stress ($\sigma$):** Defined as the force ($F$) applied per unit cross-sectional area ($A$).
$$ \sigma = \frac{F}{A} $$
* **Tensile Strain ($\varepsilon$):** Defined as the fractional change in length ($\Delta l$) relative to the original length ($l$).
$$ \varepsilon = \frac{\Delta l}{l} $$

**Young's Modulus ($E$)**, also known as the modulus of elasticity, quantifies a material's stiffness in the initial linear elastic region of its stress-strain curve. It is the ratio of tensile stress to tensile strain:
$$ E = \frac{\sigma}{\varepsilon} = \frac{F/A}{\Delta l/l} $$
This equation can be rearranged to express the force required for a given extension:
$$ F = \left( \frac{AE}{l} \right) \Delta l $$
This form is analogous to Hooke's law, $F = kx$, where the term $\left( \frac{AE}{l} \right)$ represents an effective spring constant $k_{\text{eff}}$ for the material bar. This implies that within the elastic regime, a solid bar under tension behaves similarly to an ideal spring, with its "springiness" determined by its cross-sectional area ($A$), Young's modulus ($E$), and length ($l$).
### 3) Reading a stress-strain curve: elastic limit, yield, hardening, necking, fracture
The stress-strain curve provides a comprehensive overview of a material's mechanical behaviour under increasing load.

Starting from the origin ($O$), the curve typically exhibits several distinct regions:
* **Linear Elastic Region (O to B):** In this initial segment, stress is directly proportional to strain, and the material returns to its original dimensions upon removal of the load. The slope of this linear portion is defined as Young's Modulus ($E$).
* **Elastic Limit (B) and Yield Point (C):** Beyond point B, the material starts to undergo permanent, or **plastic**, deformation. Point C, the yield point, specifically marks the onset of this irreversible deformation.
* **Plastic Deformation:** In this regime, the material's internal structure changes permanently. At a microscopic level, this involves the movement of defects called dislocations within the crystal lattice, leading to the irreversible slipping of atomic planes past one another.
* **Strain (Work) Hardening (towards F):** As plastic deformation continues, the material can become stiffer and harder. This occurs because the movement and accumulation of dislocations impede further slip, increasing the material's resistance to deformation. A common example is bending a copper wire, which becomes harder and more brittle if re-bent due to this work hardening.
* **Necking and Fracture (F to G):** In the final stages of tensile loading, the material begins to thin locally, a phenomenon known as necking. This localized reduction in cross-sectional area leads to a rapid increase in true stress until the material ultimately fractures at point G.
### 4) Quantitative elasticity: extensions and stored energy
#### 4.1 Extensions under load: order-of-magnitude checks
The relationship $F = \left( \frac{AE}{l} \right) \Delta l$ can be rearranged to calculate the extension $\Delta l = \frac{Fl}{AE}$. This formula is crucial for estimating deformations under various loads. For instance, a $4.5\,\text{m}$ copper wire with a diameter of $120\,\mu\text{m}$ subjected to loads between $50\,\text{g}$ and $150\,\text{g}$ will experience elastic extensions on the order of $1\,\text{mm}$ per added load. Similarly, a $1500\,\text{kg}$ car suspended on a $2\,\text{m}$ steel cable with a $10\,\text{mm}$ diameter (where $E \approx 200\,\text{GPa}$) would cause the cable to extend by approximately $2\,\text{mm}$. These calculations highlight that extensions in metre-scale metallic structures under typical loads are often in the millimetre range, which is useful for performing back-of-the-envelope checks to assess the physical reasonableness of results.
> **⚠️ Exam Alert!** The lecturer explicitly stated: "This is not so different to the kind of questions you get in the multiple choice exam. In fact, this resembles one from last year, I think." Students should be prepared for calculations involving the extension of materials like steel cables supporting vehicles.
#### 4.2 Energy stored in elastic extension
When a material is stretched within its elastic limit, work is done against the interatomic forces, and this energy is stored as elastic potential energy in the stretched bonds. The work ($W$) done in extending a material from zero to an extension $\Delta l$ can be derived by integrating the force over the displacement:
$$ W = \int F \, d(\Delta l) $$
Substituting $F = \left( \frac{AE}{l} \right) \Delta l$, the integral becomes:
$$ W = \int_0^{\Delta l} \left( \frac{AE}{l} \right) \Delta l' \, d(\Delta l') = \frac{AE}{l} \left[ \frac{(\Delta l')^2}{2} \right]_0^{\Delta l} = \frac{AE}{2l} (\Delta l)^2 $$
This stored elastic energy, for the car-cable example, amounts to approximately $23\,\text{J}$.
> **⚠️ Exam Alert!** The lecturer explicitly stated: "This sort of question is precisely what appeared in last year's multiple choice exam." Students should be proficient in computing stored elastic energy given the extension and material dimensions.
#### 4.3 Live demo narrative: spotting the yield point with a copper wire
A live demonstration involving a long copper wire suspended with a ruler illustrates the transition from elastic to plastic deformation. Initially, the addition of $50\,\text{g}$ weights causes visible elastic extensions, typically around $1.5\,\text{mm}$ to $2\,\text{mm}$ per weight. Up to a total load of approximately $150\,\text{g}$ to $200\,\text{g}$, the wire stretches reversibly. However, beyond this point, the wire begins to stretch continuously and rapidly, indicating that the **yield strength** has been exceeded and plastic deformation has commenced. Upon removal of the loads, the wire does not return to its original baseline length, confirming permanent deformation.
The yield strength for copper is typically in the order of tens of megapascals ($\text{MPa}$). Using the relationship $\sigma_y \approx F_y/A$, one can estimate the maximum "safe" load ($F_y$) that a wire of a given cross-sectional area ($A$) can withstand before yielding. Microscopically, in the elastic region, atomic bonds stretch reversibly. Beyond the yield point, dislocations move and atomic planes slip, leading to permanent set and potentially subsequent strain hardening.
### 5) From atoms to E: deriving Young’s modulus from the interatomic potential
The macroscopic elastic properties of a solid can be derived from its fundamental interatomic potential. This approach re-establishes the "atoms-on-springs" model.


The interatomic potential $V(r)$ describes the energy of interaction between two atoms as a function of their separation $r$. Key features of this potential include:
* An equilibrium separation $a_0$, corresponding to the minimum of the potential well, where the net force between atoms is zero.
* A well depth $\varepsilon$, representing the bond or separation energy required to fully separate the atoms.
The interatomic force $F$ is related to the potential by $F = dV/dr$. For small displacements $\Delta r$ around the equilibrium separation $a_0$, the change in force $\Delta F$ can be approximated linearly:
$$ \Delta F \approx \Delta r \left( \frac{dF}{dr} \right)_{r=a_0} = \Delta r \left( \frac{d^2V}{dr^2} \right)_{r=a_0} $$
This expression $\left( \frac{d^2V}{dr^2} \right)_{r=a_0}$ represents the "stiffness" of a single bond, analogous to a spring constant.
To bridge the microscopic and macroscopic scales, the following relationships are used:
* The force per bond ($f$) is related to the macroscopic force ($F$) and cross-sectional area ($A$) by considering the density of bonds across that area: $f = F \left( \frac{a_0^2}{A} \right)$.
* The macroscopic extension ($\Delta l$) is related to the bond extension ($\Delta r$) by considering the number of bonds in series along the length ($l$): $\Delta l = \Delta r \left( \frac{l}{a_0} \right)$.
Substituting these microscopic expressions into the definition of Young's Modulus $E = (F/A) / (\Delta l/l)$ yields:
$$ E = \frac{1}{a_0} \left( \frac{d^2V}{dr^2} \right)_{r=a_0} $$
This fundamental equation relates the macroscopic Young's Modulus directly to the curvature of the interatomic potential at the equilibrium separation.
For a worked example, consider solid argon, which can be modelled by a Lennard-Jones potential. For this potential, the second derivative at equilibrium is $\left( \frac{d^2V}{dr^2} \right)_{r=a_0} = \frac{72\varepsilon}{a_0^2}$. Substituting this into the derived equation for $E$ gives $E = \frac{72\varepsilon}{a_0^3}$. Using typical values for argon ($a_0 \approx 3.7 \times 10^{-10}\,\text{m}$ and $\varepsilon \approx 1.7 \times 10^{-21}\,\text{J}$), the calculated Young's modulus is approximately $2.4\,\text{GPa}$. This value is about a factor of two smaller than the measured value of $4.8\,\text{GPa}$. The discrepancy arises because this simplified "independent chains" model neglects the lateral coupling and interactions between neighbouring rows of atoms, which contribute to the overall stiffness. Despite this, it provides a remarkably accurate order-of-magnitude estimate from first principles.
### 6) Entropic elasticity: why rubber heats when stretched and contracts when heated
Rubber, a polymer, exhibits a unique form of elasticity driven primarily by entropy rather than direct bond stretching. At a microscopic level, rubber consists of long polymer chains that naturally prefer a tangled, disordered state, which corresponds to a high-entropy configuration. When a rubber band is stretched, these chains are forced to align, resulting in a more ordered, lower-entropy state.
This entropic effect explains the observed elastocaloric phenomena:
* **Stretching and Heating:** When a rubber band is stretched rapidly, its internal entropy decreases. For the total entropy of the universe to uphold the Second Law of Thermodynamics (i.e., $\Delta S_{\text{universe}} \geq 0$), the system must expel heat to its surroundings. This expelled heat is perceived as warmth. If the stretched band is held, it gradually cools back to ambient temperature as it exchanges heat with the surroundings.
* **Relaxation and Cooling:** Conversely, when a stretched rubber band is quickly released, the polymer chains spontaneously return to their high-entropy, tangled state. This increase in the system's entropy leads to the absorption of heat from the surroundings, causing the band to feel cool.
* **Heating a Hanging Band:** Unlike metals, which expand and lengthen when heated due to increased atomic vibrations, a hanging rubber band contracts when heated. The added thermal energy increases the number of accessible microstates for the polymer chains, driving them to "recrumple" towards a state of higher entropy. This entropic drive causes the band to shorten and lift any attached weight, a phenomenon that can be visibly demonstrated with a heat gun.
### 7) Consolidation and next steps
This course has explored the mechanical properties of materials, bridging macroscopic observations with microscopic models.
* **Macroscopic and Quantitative Tools:** We defined stress ($\sigma = F/A$), strain ($\varepsilon = \Delta l/l$), and Young's modulus ($E = \sigma/\varepsilon$). We analysed the stress-strain curve, identifying regions of linear elasticity, yield, plastic deformation, strain hardening, necking, and fracture. Quantitative tools derived include the extension of a bar under load ($\Delta l = Fl/(AE)$) and the elastic energy stored within it ($W = (AE/2l) (\Delta l)^2$), allowing for order-of-magnitude estimates that are typically in the millimetre range for metre-scale metals.
* **Microscopic Models and Thermodynamics:** We linked Young's modulus to the curvature of the interatomic potential at equilibrium ($E = (1/a_0) (d^2V/dr^2)|_{r=a_0}$), demonstrating that the "atoms-as-springs" model provides a powerful first-principles understanding of material stiffness. Furthermore, the concept of entropic elasticity was used to explain the unique behaviour of rubber, specifically its heating upon stretching and contraction upon heating, in terms of changes in polymer chain disorder and the Second Law of Thermodynamics.
This concludes the new material for the course. A two-hour revision session, covering both Mechanics and Properties of Matter, will replace the cancelled problems class next week. The lecturer will highlight key slides and topics relevant for the upcoming exam during this session.
## Key takeaways
* Stress-strain: $\sigma = F/A$, $\varepsilon = \Delta l/l$. In the elastic region, $\sigma \propto \varepsilon$ with slope $E$; beyond the yield point, plastic deformation sets in via dislocation motion, followed by strain hardening, necking, and fracture.
* A bar in tension behaves like a spring with an effective spring constant $k_{\text{eff}} = AE/l$; extensions $\Delta l = Fl/(AE)$ are typically millimetres for metre-scale metals under practical loads.
* Elastic energy stored by stretching is $W = (AE/2l) (\Delta l)^2$.
* Microscopic origin of stiffness: $E = (1/a_0) (d^2V/dr^2)|_{r=a_0}$. For Lennard-Jones solids (e.g., Ar), this provides the correct order of magnitude; discrepancies are explained by neglecting neighbour coupling.
* Rubber’s elasticity is entropic: stretching lowers the polymer chains' entropy and causes heat expulsion; heating increases entropy and results in contraction under load.
* Administrative: this is the final new-content lecture; a two-hour revision session (covering Mechanics + Properties of Matter) replaces the cancelled problems class and will highlight likely exam-relevant material.




