Lecture 10: Reversible Processes and Adiabatic Expansion (Diesel Engine)
0) Orientation, admin, and quick review

This lecture builds on previous discussions of the First Law of Thermodynamics, work, heat, and ideal gas differentials. It introduces the definition of reversible versus irreversible processes, methods for computing work in isothermal and adiabatic processes, and the derivation and application of adiabatic relations ($PV^\gamma$ and $TV^{\gamma-1}$). These principles are then connected to the operation of the diesel engine. The concept of enthalpy, $H = U + PV$, is also introduced, which will be crucial for understanding later thermodynamic cycles and the Second Law.
Regarding administrative matters, students are invited to participate in an optional, extra-curricular research project focusing on first-year physics learning. This project aims to gather feedback on the curriculum and identify areas where teaching methods could be improved.
The First Law of Thermodynamics states that the internal energy $U$ is a state function, meaning its value depends only on the current state of the system, not the path taken to reach it. Heat ($Q$) and work ($W$), however, are processes of energy transfer. In this course, the First Law is primarily expressed in its differential form as $dQ = dU + PdV$, where $PdV$ represents the work done by the system. This convention will be consistently applied in derivations throughout this lecture.
1) What thermodynamic reversibility really means
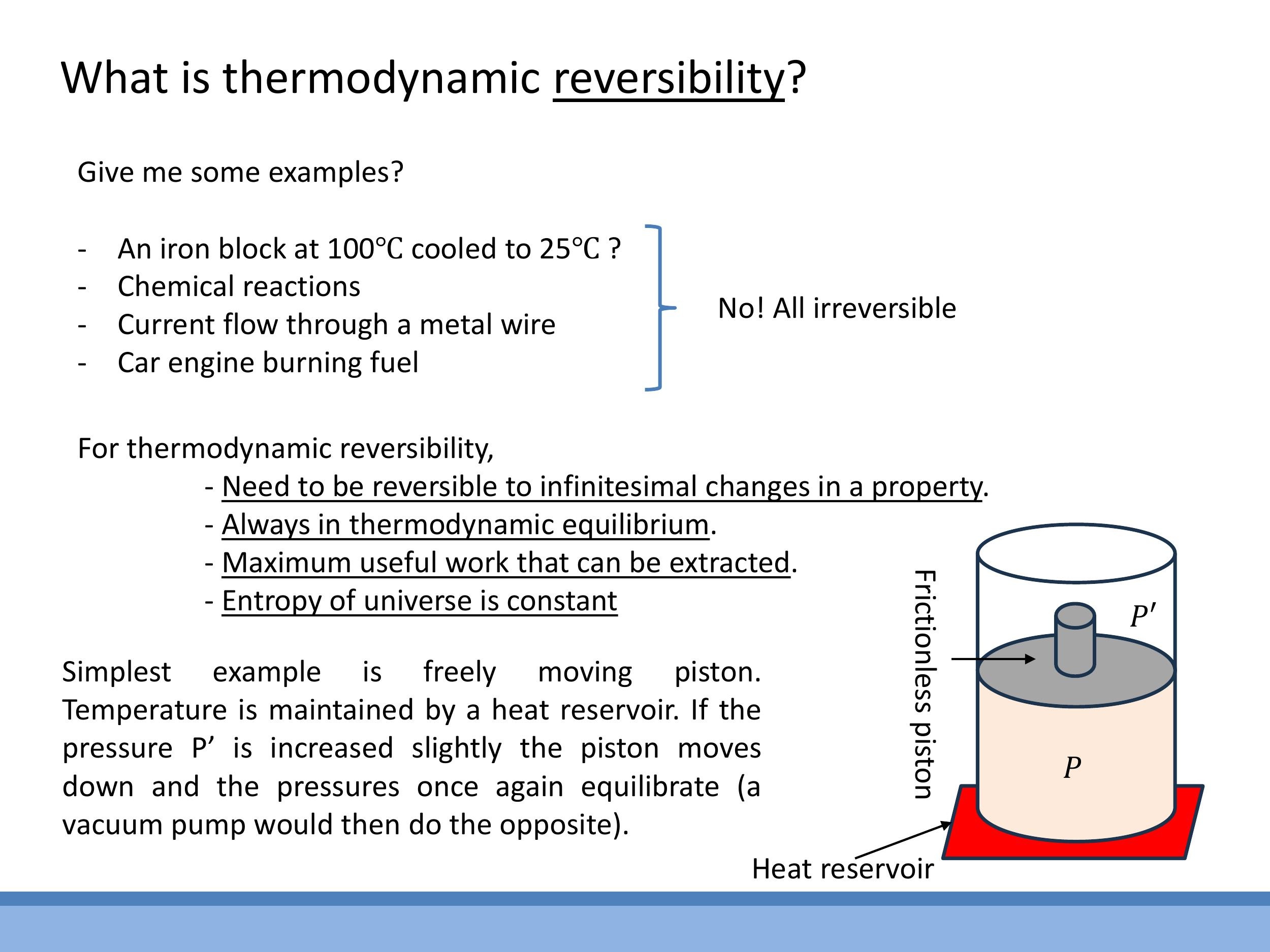
Thermodynamic reversibility is an idealised concept crucial for understanding the maximum possible efficiency of thermodynamic processes. Most everyday processes are irreversible. Examples include a hot iron block cooling in room air, chemical reactions, the steady flow of current through a wire, or the combustion of fuel in an engine. These processes are irreversible because a small, infinitesimal change in the surroundings cannot reverse their direction. For instance, if a $100 \, ^\circ\text{C} $ block is cooling, a $ 0.1 \, ^\circ\text{C}$ increase in the ambient air temperature will not cause the block to start warming up again.
An ideal reversible process adheres to specific conditions. The system must remain in thermodynamic equilibrium throughout the process, meaning its macroscopic properties are unchanging and balanced. It must also be reversible to infinitesimal changes; a tiny adjustment in a system property or its surroundings should be able to reverse the direction of the process. Reversible processes are theoretical constructs that extract the maximum useful work possible from a given energy transfer. A key characteristic, to be fully explored later, is that a perfectly reversible process leaves the total entropy of the universe (system plus surroundings) unchanged.
A frictionless piston in equilibrium with a heat reservoir provides a physical model for a reversible process. If the piston is in equilibrium, an infinitesimal increase in the reservoir's temperature will cause the piston to move upwards, while an infinitesimal decrease will cause it to move downwards. This demonstrates the system's responsiveness to tiny changes, fulfilling the criteria for reversibility.
2) Work in P-V processes: from forces to dW = PdV
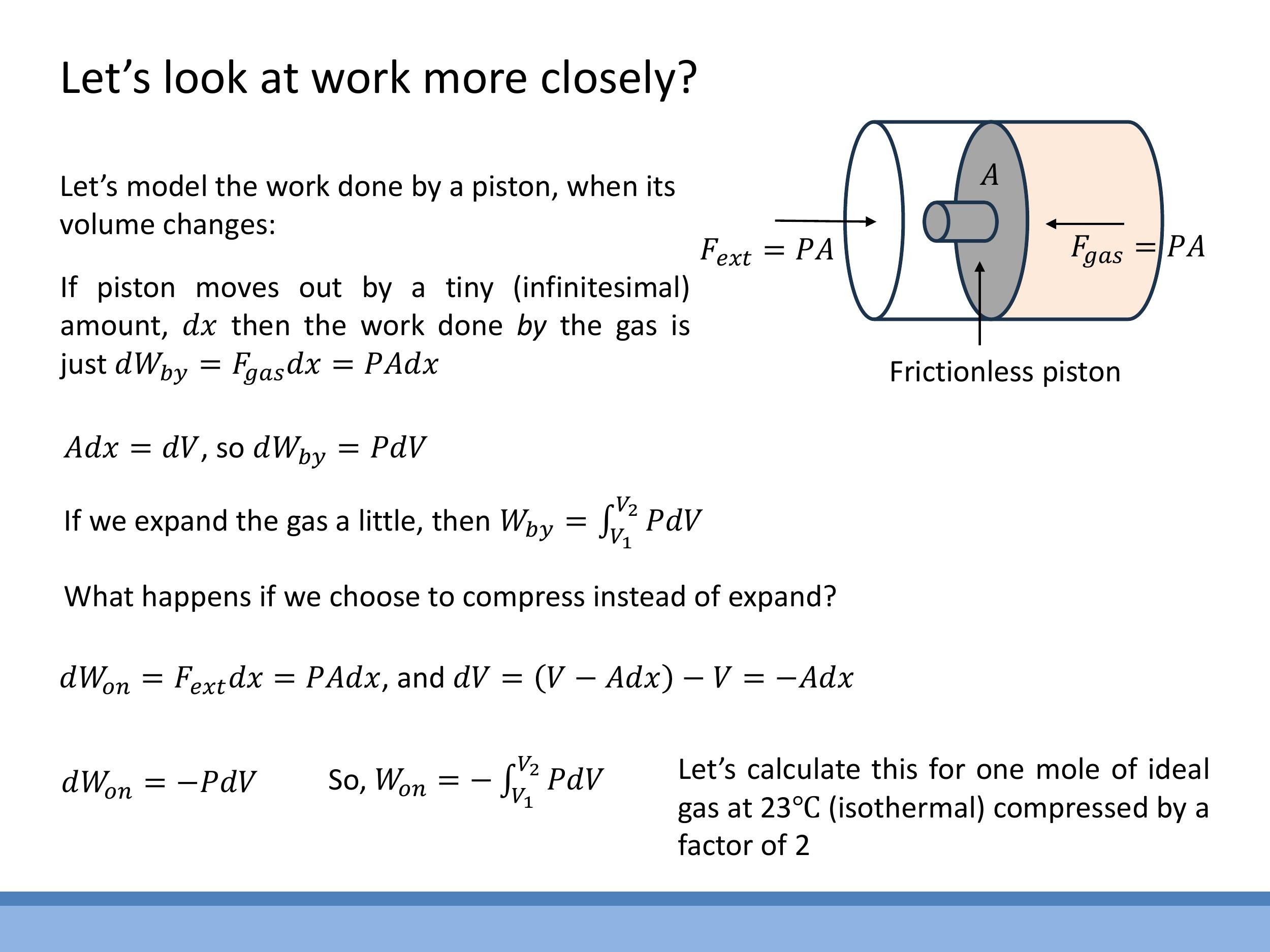
The work done during a thermodynamic process involving a change in volume can be derived from fundamental mechanical principles. When a gas expands, it exerts a force on a piston, performing work by the gas. If the piston moves an infinitesimal distance $dx$, the work done is $dW_{\text{by}} = F_{\text{gas}} \, dx $. Since force is pressure times area ($ F_{\text{gas}} = P A $), this becomes $ dW_{\text{by}} = P A \, dx $. Recognising that the product of the area and the infinitesimal displacement ($ A \, dx $) is the infinitesimal change in volume ($ dV $), the work done by the gas is given by $ dW_{\text{by}} = P \, dV$.
Conversely, when work is done on the gas, such as during compression, an external force pushes the piston inwards. In this case, the infinitesimal change in volume $dV$ is negative (since $dx$ is in the opposite direction of the force exerted by the gas). Therefore, the work done on the gas is $dW_{\text{on}} = -P \, dV$.
To find the total work done over a process where the volume changes from $V_1$ to $V_2$, these infinitesimal work elements are integrated. The total work done by the gas is $W_{\text{by}} = \int_{V_1}^{V_2} P \, dV$, and the total work done on the gas is $W_{\text{on}} = -\int_{V_1}^{V_2} P \, dV $. On a pressure-volume ($ P-V$) diagram, the magnitude of the work done during a process is represented by the area under the curve of the process path. The sign depends on whether the volume is increasing (work by the gas) or decreasing (work on the gas).
3) Isothermal work for an ideal gas and what the area means
For an ideal gas undergoing a reversible isothermal process, the temperature $T$ remains constant. For one mole of an ideal gas, the ideal gas law states $P V = R T$, which can be rearranged to express pressure as $P = \frac{R T}{V}$. This expression for $P$ can be substituted into the integral for work done on the gas during a volume change from $V_1$ to $V_2$:
$$
W_{\text{on}} = -\int_{V_1}^{V_2} P \, dV = -\int_{V_1}^{V_2} \frac{R T}{V} \, dV
$$
Since $R$ and $T$ are constant for an isothermal process, they can be taken out of the integral:
$$ W_{\text{on}} = -R T \int_{V_1}^{V_2} \frac{1}{V} \, dV = -R T \left[ \ln(V) \right] {V_1}^{V_2} = -R T \left( \ln(V_2) - \ln(V_1) \right) $$
Using logarithm properties, this simplifies to:
$$ W {\text{on}} = -R T \ln\left(\frac{V_2}{V_1}\right) = R T \ln\left(\frac{V_1}{V_2}\right) $$
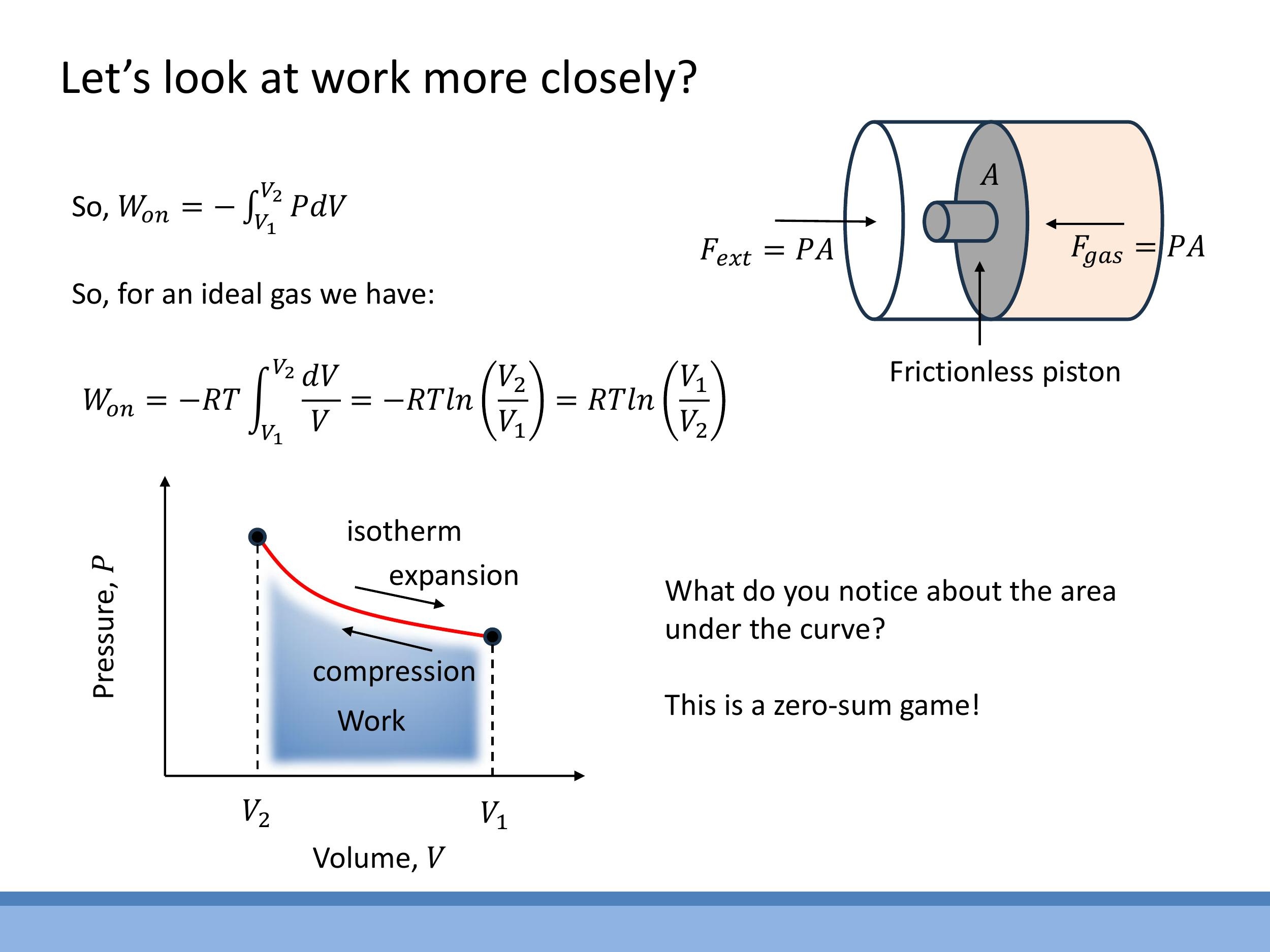
An example calculation for compressing $1 \, \text{mol} $ of an ideal gas at $ 23 \, ^\circ\text{C} $ (approximately $ 300 \, \text{K} $) by a factor of $ 2 $ ($ V_1/V_2 = 2 $) yields $ W_{\text{on}} \approx (8.314 \, \text{J mol}^{-1}\text{K}^{-1})(300 \, \text{K})\ln(2) \approx 1.7 \times 10^3 \, \text{J}$.
On a $P-V$ diagram, an isotherm for an ideal gas follows a hyperbolic curve. The work done during the process is represented by the area under this curve. If a gas expands isothermally and then compresses back to its original state along the same isotherm, the work done during expansion is positive (by the gas), and the work done during compression is negative (by the gas). The net work done over such a cycle is zero, indicating that no net useful work is extracted from the system.
⚠️ Exam Alert! The lecturer explicitly stated: "This is not so difficult but not so different to the kind of question that you might get in the multiple choice test in December. It's not so different. Something like this, I've asked before." Students should be prepared to perform calculations of isothermal work for an ideal gas.
4) Adding friction: why loops appear and where the work goes
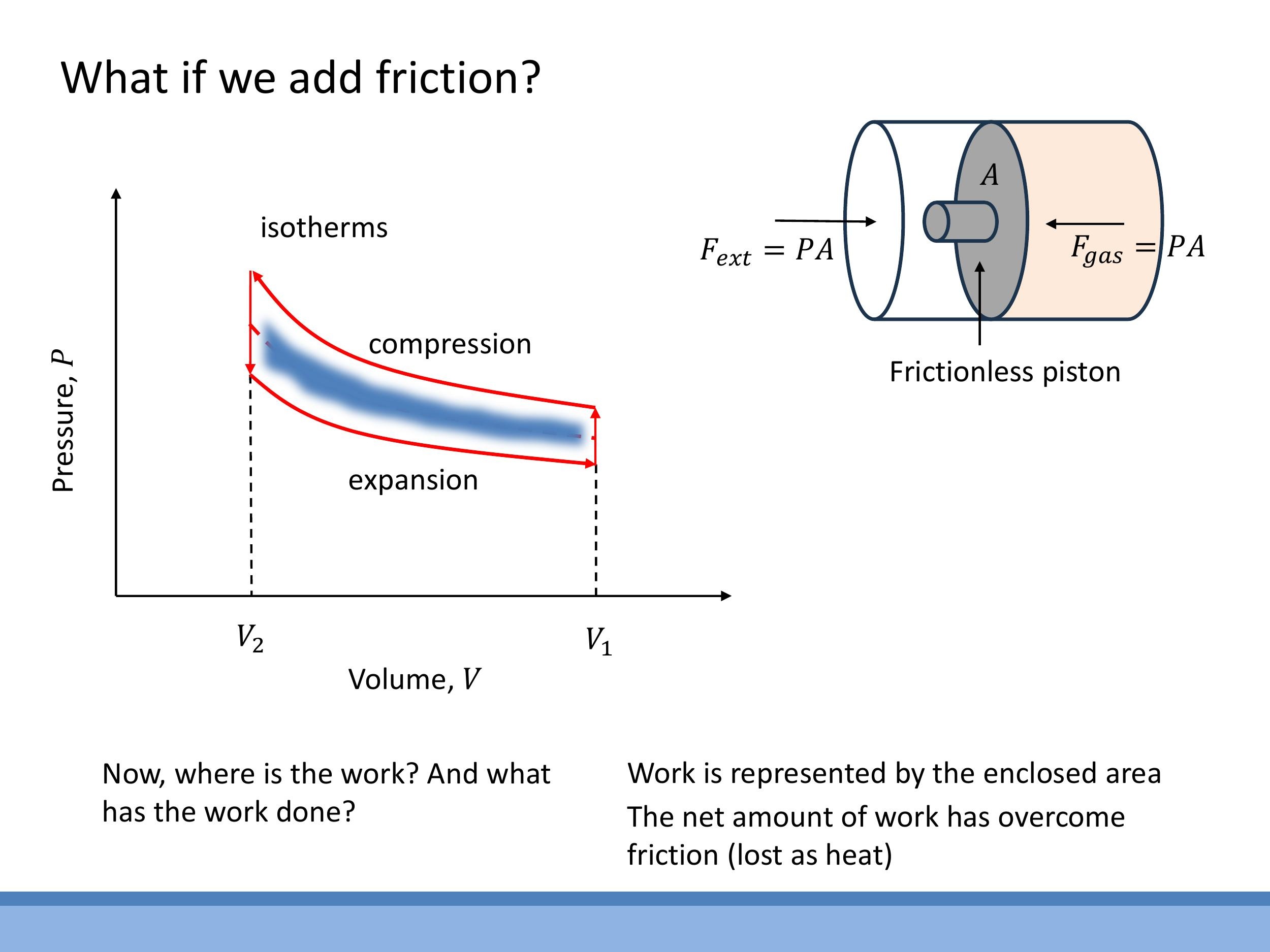
In real thermodynamic processes, especially those involving mechanical motion such as a piston, friction is always present. When friction is introduced, the compression and expansion of a gas no longer follow the same path on a $P-V$ diagram. The work done during compression (on the system) will be greater than the work recovered during expansion (by the system). This difference in paths creates a closed loop on the $P-V$ diagram.
The area enclosed by this loop represents the net work done during the cycle. However, in the presence of friction, this net work is not useful output; instead, it is dissipated as heat, overcoming the frictional forces. This highlights the irreversibility of real processes: energy is "lost" to the surroundings as heat, reducing the efficiency of work extraction. A truly reversible process, by contrast, would follow a single path, maximising the useful work.
5) Adiabatic processes: definition and P-V shape
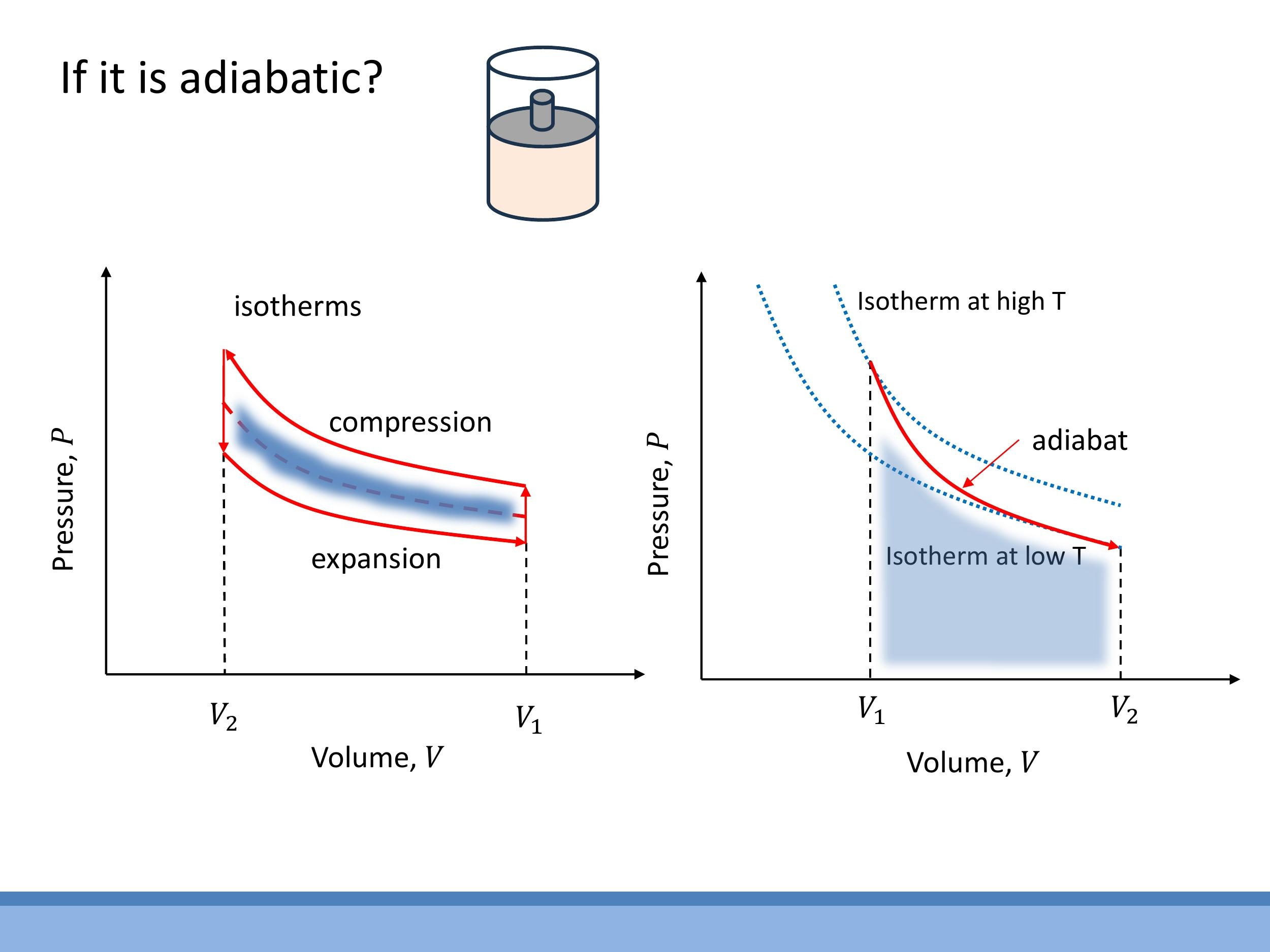
An adiabatic process is defined as a thermodynamic process in which no heat is exchanged between the system and its surroundings, meaning $dQ = 0$. Such processes are typically approximated by rapid expansions or compressions, where there is insufficient time for significant heat transfer, or by systems that are well-insulated.
On a $P-V$ diagram, an adiabatic curve (an adiabat) is steeper than an isothermal curve (an isotherm). This difference arises because during an adiabatic process, the temperature of the gas changes. For example, in an adiabatic compression, work is done on the gas, increasing its internal energy and thus its temperature without any heat being removed. This causes the gas to move to a higher-temperature isotherm. Conversely, in an adiabatic expansion, the gas does work, decreasing its internal energy and temperature, moving it to a lower-temperature isotherm. The steeper slope of the adiabat reflects this additional temperature change influencing the pressure-volume relationship.
6) Deriving the reversible adiabatic relation PV^γ = constant


The relationship between pressure and volume for a reversible adiabatic process of an ideal gas can be derived by combining the First Law of Thermodynamics with the ideal gas law and specific heat definitions.
The starting ingredients are:
- First Law of Thermodynamics (for adiabatic process): Since $dQ = 0$, the First Law $dQ = dU + PdV$ becomes $0 = dU + PdV$, or $dU = -PdV$.
- Internal Energy of an Ideal Gas: For an ideal gas, the change in internal energy is related to the change in temperature by $dU = C_V dT$, where $C_V$ is the molar specific heat at constant volume.
- Differential Ideal Gas Law (for 1 mole): Differentiating $PV = RT$ yields $P \, dV + V \, dP = R \, dT$.
- Mayer's Relation: This relates the molar specific heats at constant pressure ($C_P$) and constant volume ($C_V$): $R = C_P - C_V$.
- Ratio of Specific Heats: Defined as $\gamma \equiv C_P/C_V$.
From the adiabatic First Law and the internal energy relation, we have $C_V dT = -PdV$.
Substituting $R = C_P - C_V$ into the differential ideal gas law gives $(C_P - C_V)dT = VdP + PdV$.
Now, substitute $PdV = -C_V dT$ into this equation:
$(C_P - C_V)dT = VdP - C_V dT$
The $-C_V dT$ terms on both sides cancel, leading to a second key relation: $C_P dT = VdP$.
We now have two expressions for $dT$:
$dT = -\frac{P \, dV}{C_V} $ and $ dT = \frac{V \, dP}{C_P}$.
Equating these gives:
$-\frac{P \, dV}{C_V} = \frac{V \, dP}{C_P}$
Rearranging and introducing $\gamma = C_P/C_V$:
$\frac{C_P}{C_V} = -\frac{V}{P}\frac{dP}{dV}$
$\gamma = -\frac{V}{P}\frac{dP}{dV}$
To solve this, we separate the variables:
$\gamma \frac{dV}{V} = -\frac{dP}{P}$
Integrating both sides from an initial state $(P_1, V_1)$ to a final state $(P_2, V_2)$:
$\int_{V_1}^{V_2} \gamma \frac{dV}{V} = -\int_{P_1}^{P_2} \frac{dP}{P}$
$\gamma \left[ \ln(V) \right] {V_1}^{V_2} = - \left[ \ln(P) \right] {P_1}^{P_2}$
$\gamma \ln\left(\frac{V_2}{V_1}\right) = - \ln\left(\frac{P_2}{P_1}\right)$
Using logarithm properties ($\alpha \ln x = \ln x^\alpha$ and $-\ln x = \ln(1/x)$):
$\ln\left(\left(\frac{V_2}{V_1}\right)^\gamma\right) = \ln\left(\frac{P_1}{P_2}\right)$
Exponentiating both sides yields the reversible adiabatic relation:
$P_1 V_1^\gamma = P_2 V_2^\gamma = \text{constant}$
The value of $\gamma$ depends on the type of gas. For monatomic ideal gases, $\gamma = 5/3 \approx 1.67$. For diatomic ideal gases (like air at room temperature), $\gamma = 7/5 = 1.4$.
7) Temperature-volume relation for adiabatic processes

From the derived adiabatic relation $PV^\gamma = \text{constant}$ and the ideal gas law $P = \frac{RT}{V}$ (for one mole), a direct relationship between temperature and volume can be obtained.
Substitute $P = \frac{RT}{V}$ into the adiabatic equation:
$\left(\frac{RT}{V}\right) V^\gamma = \text{constant}$
$RT V^{\gamma-1} = \text{constant}$
Since $R$ is a constant, this implies that $T V^{\gamma-1} = \text{constant}$ for a reversible adiabatic process.
This relation can be written in terms of initial and final states as:
$T_1 V_1^{\gamma-1} = T_2 V_2^{\gamma-1}$
or, more practically for calculations:
$T_2 = T_1 \left(\frac{V_1}{V_2}\right)^{\gamma-1}$
This formula is particularly useful for quickly estimating the temperature change during adiabatic compression or expansion, as the exponent $\gamma-1$ directly controls the magnitude of the temperature rise or fall.
8) Application: adiabatic compression in the diesel engine (+ live demo)

The principle of adiabatic compression is fundamental to the operation of a diesel engine. In a diesel engine, air is rapidly compressed to a very high temperature. This significant temperature increase is sufficient to ignite the injected fuel without the need for a spark plug.
Consider an estimate for air, which is primarily a diatomic gas, so $\gamma \approx 1.4$. If air starts at room temperature ($T_1 \approx 300 \, \text{K} $) and is compressed to one-tenth of its original volume ($ V_1/V_2 = 10 $), the final temperature $ T_2 $ can be calculated using the relation $ T_2 = T_1 (V_1/V_2)^{\gamma-1}$:
$T_2 = 300 \, \text{K} \times (10)^{(1.4 - 1)} = 300 \, \text{K} \times 10^{0.4}$
$T_2 \approx 300 \, \text{K} \times 2.51 \approx 753 \, \text{K}$
This temperature, approximately $480 \, ^\circ\text{C} $, is ample to ignite diesel fuel. Real diesel engines often have higher compression ratios, sometimes up to $ 16:1$, leading to even greater final temperatures.
This phenomenon can be dramatically demonstrated with a "fire piston". The setup involves a transparent cylinder containing air and a small piece of cotton wool. When the piston is very rapidly compressed, the air inside heats sufficiently to ignite the cotton wool, which flashes brightly. The "very rapid" compression approximates an adiabatic process, providing visual proof of the substantial temperature rise.
9) Introduction to enthalpy: H = U + PV

Enthalpy, denoted by $H$, is a thermodynamic state function defined as $H \equiv U + PV$, where $U$ is the internal energy, $P$ is the pressure, and $V$ is the volume of the system. Since $U$, $P$, and $V$ are all state functions, $H$ is also a state function, meaning its value depends only on the current state of the system, not the path taken to reach that state.
Enthalpy is particularly useful for analysing processes that occur at constant pressure. In such a process, the change in enthalpy, $\Delta H$, is equal to the heat $Q$ transferred into or out of the system. This makes enthalpy a convenient quantity for linking a measurable heat transfer to a state function, especially in open systems or flow processes where volume changes occur against a constant external pressure (e.g., chemical reactions in open containers or continuous flow systems). Enthalpy will be extensively used in the study of the Second Law of Thermodynamics and the analysis of various thermodynamic cycles.
Key takeaways
Reversibility is an idealised concept for thermodynamic processes where the system remains in quasi-static equilibrium and responds to infinitesimal changes. Such processes extract the maximum useful work and leave the total entropy of the universe unchanged, in contrast to everyday irreversible processes which always increase total entropy.
For gases, the infinitesimal work done by the gas is $dW_{\text{by}} = P \, dV$, while the work done on the gas is $dW_{\text{on}} = -P \, dV $. The area under the $ P-V $ curve represents the magnitude of the work. For an ideal gas undergoing an isothermal expansion and compression along the same path, the net work is zero. When friction is present, the compression and expansion paths diverge, forming a loop on the $ P-V$ diagram whose enclosed area represents work lost as heat due to irreversibility.
Adiabatic processes are characterised by no heat exchange ($dQ = 0$). For an ideal gas undergoing a reversible adiabatic process, two key relations hold: $P V^\gamma = \text{constant}$ and $T V^{\gamma-1} = \text{constant}$, where $\gamma = C_P/C_V$ is the ratio of specific heats. For diatomic gases like air at room temperature, $\gamma \approx 1.4$.
A practical application of adiabatic compression is the diesel engine, where rapid compression of air raises its temperature sufficiently to ignite fuel without a spark. For instance, a $10$ -fold volume reduction from $300 \, \text{K} $ results in a temperature of approximately $ 750 \, \text{K} $ (about $ 480 \, ^\circ\text{C}$).
Enthalpy, $H = U + PV$, is a state function that is particularly useful for processes occurring at constant pressure, where the change in enthalpy, $\Delta H$, directly equals the heat $Q$ transferred. This provides a measurable link to a state function, which is valuable in the analysis of thermodynamic cycles and in the context of the Second Law.
## Lecture 10: Reversible Processes and Adiabatic Expansion (Diesel Engine)
### 0) Orientation, admin, and quick review

This lecture builds on previous discussions of the First Law of Thermodynamics, work, heat, and ideal gas differentials. It introduces the definition of reversible versus irreversible processes, methods for computing work in isothermal and adiabatic processes, and the derivation and application of adiabatic relations ($PV^\gamma$ and $TV^{\gamma-1}$). These principles are then connected to the operation of the diesel engine. The concept of enthalpy, $H = U + PV$, is also introduced, which will be crucial for understanding later thermodynamic cycles and the Second Law.
Regarding administrative matters, students are invited to participate in an optional, extra-curricular research project focusing on first-year physics learning. This project aims to gather feedback on the curriculum and identify areas where teaching methods could be improved.
The First Law of Thermodynamics states that the internal energy $U$ is a state function, meaning its value depends only on the current state of the system, not the path taken to reach it. Heat ($Q$) and work ($W$), however, are processes of energy transfer. In this course, the First Law is primarily expressed in its differential form as $dQ = dU + PdV$, where $PdV$ represents the work done *by* the system. This convention will be consistently applied in derivations throughout this lecture.
### 1) What thermodynamic reversibility really means

Thermodynamic reversibility is an idealised concept crucial for understanding the maximum possible efficiency of thermodynamic processes. Most everyday processes are irreversible. Examples include a hot iron block cooling in room air, chemical reactions, the steady flow of current through a wire, or the combustion of fuel in an engine. These processes are irreversible because a small, infinitesimal change in the surroundings cannot reverse their direction. For instance, if a $100\,^\circ\text{C}$ block is cooling, a $0.1\,^\circ\text{C}$ increase in the ambient air temperature will not cause the block to start warming up again.
An ideal reversible process adheres to specific conditions. The system must remain in thermodynamic equilibrium throughout the process, meaning its macroscopic properties are unchanging and balanced. It must also be reversible to infinitesimal changes; a tiny adjustment in a system property or its surroundings should be able to reverse the direction of the process. Reversible processes are theoretical constructs that extract the maximum useful work possible from a given energy transfer. A key characteristic, to be fully explored later, is that a perfectly reversible process leaves the total entropy of the universe (system plus surroundings) unchanged.
A frictionless piston in equilibrium with a heat reservoir provides a physical model for a reversible process. If the piston is in equilibrium, an infinitesimal increase in the reservoir's temperature will cause the piston to move upwards, while an infinitesimal decrease will cause it to move downwards. This demonstrates the system's responsiveness to tiny changes, fulfilling the criteria for reversibility.
### 2) Work in P-V processes: from forces to dW = PdV

The work done during a thermodynamic process involving a change in volume can be derived from fundamental mechanical principles. When a gas expands, it exerts a force on a piston, performing work *by* the gas. If the piston moves an infinitesimal distance $dx$, the work done is $dW_{\text{by}} = F_{\text{gas}} \, dx$. Since force is pressure times area ($F_{\text{gas}} = P A$), this becomes $dW_{\text{by}} = P A \, dx$. Recognising that the product of the area and the infinitesimal displacement ($A \, dx$) is the infinitesimal change in volume ($dV$), the work done by the gas is given by $dW_{\text{by}} = P \, dV$.
Conversely, when work is done *on* the gas, such as during compression, an external force pushes the piston inwards. In this case, the infinitesimal change in volume $dV$ is negative (since $dx$ is in the opposite direction of the force exerted *by* the gas). Therefore, the work done *on* the gas is $dW_{\text{on}} = -P \, dV$.
To find the total work done over a process where the volume changes from $V_1$ to $V_2$, these infinitesimal work elements are integrated. The total work done *by* the gas is $W_{\text{by}} = \int_{V_1}^{V_2} P \, dV$, and the total work done *on* the gas is $W_{\text{on}} = -\int_{V_1}^{V_2} P \, dV$. On a pressure-volume ($P-V$) diagram, the magnitude of the work done during a process is represented by the area under the curve of the process path. The sign depends on whether the volume is increasing (work by the gas) or decreasing (work on the gas).
### 3) Isothermal work for an ideal gas and what the area means

For an ideal gas undergoing a reversible isothermal process, the temperature $T$ remains constant. For one mole of an ideal gas, the ideal gas law states $P V = R T$, which can be rearranged to express pressure as $P = \frac{R T}{V}$. This expression for $P$ can be substituted into the integral for work done *on* the gas during a volume change from $V_1$ to $V_2$:
$$ W_{\text{on}} = -\int_{V_1}^{V_2} P \, dV = -\int_{V_1}^{V_2} \frac{R T}{V} \, dV $$
Since $R$ and $T$ are constant for an isothermal process, they can be taken out of the integral:
$$ W_{\text{on}} = -R T \int_{V_1}^{V_2} \frac{1}{V} \, dV = -R T \left[ \ln(V) \right]_{V_1}^{V_2} = -R T \left( \ln(V_2) - \ln(V_1) \right) $$
Using logarithm properties, this simplifies to:
$$ W_{\text{on}} = -R T \ln\left(\frac{V_2}{V_1}\right) = R T \ln\left(\frac{V_1}{V_2}\right) $$
An example calculation for compressing $1\,\text{mol}$ of an ideal gas at $23\,^\circ\text{C}$ (approximately $300\,\text{K}$) by a factor of $2$ ($V_1/V_2 = 2$) yields $W_{\text{on}} \approx (8.314\,\text{J mol}^{-1}\text{K}^{-1})(300\,\text{K})\ln(2) \approx 1.7 \times 10^3\,\text{J}$.
On a $P-V$ diagram, an isotherm for an ideal gas follows a hyperbolic curve. The work done during the process is represented by the area under this curve. If a gas expands isothermally and then compresses back to its original state along the same isotherm, the work done during expansion is positive (by the gas), and the work done during compression is negative (by the gas). The net work done over such a cycle is zero, indicating that no net useful work is extracted from the system.
> **⚠️ Exam Alert!** The lecturer explicitly stated: "This is not so difficult but not so different to the kind of question that you might get in the multiple choice test in December. It's not so different. Something like this, I've asked before." Students should be prepared to perform calculations of isothermal work for an ideal gas.
### 4) Adding friction: why loops appear and where the work goes

In real thermodynamic processes, especially those involving mechanical motion such as a piston, friction is always present. When friction is introduced, the compression and expansion of a gas no longer follow the same path on a $P-V$ diagram. The work done during compression (on the system) will be greater than the work recovered during expansion (by the system). This difference in paths creates a closed loop on the $P-V$ diagram.
The area enclosed by this loop represents the net work done during the cycle. However, in the presence of friction, this net work is not useful output; instead, it is dissipated as heat, overcoming the frictional forces. This highlights the irreversibility of real processes: energy is "lost" to the surroundings as heat, reducing the efficiency of work extraction. A truly reversible process, by contrast, would follow a single path, maximising the useful work.
### 5) Adiabatic processes: definition and P-V shape

An adiabatic process is defined as a thermodynamic process in which no heat is exchanged between the system and its surroundings, meaning $dQ = 0$. Such processes are typically approximated by rapid expansions or compressions, where there is insufficient time for significant heat transfer, or by systems that are well-insulated.
On a $P-V$ diagram, an adiabatic curve (an adiabat) is steeper than an isothermal curve (an isotherm). This difference arises because during an adiabatic process, the temperature of the gas changes. For example, in an adiabatic compression, work is done on the gas, increasing its internal energy and thus its temperature without any heat being removed. This causes the gas to move to a higher-temperature isotherm. Conversely, in an adiabatic expansion, the gas does work, decreasing its internal energy and temperature, moving it to a lower-temperature isotherm. The steeper slope of the adiabat reflects this additional temperature change influencing the pressure-volume relationship.
### 6) Deriving the reversible adiabatic relation PV^γ = constant


The relationship between pressure and volume for a reversible adiabatic process of an ideal gas can be derived by combining the First Law of Thermodynamics with the ideal gas law and specific heat definitions.
The starting ingredients are:
1. **First Law of Thermodynamics (for adiabatic process):** Since $dQ = 0$, the First Law $dQ = dU + PdV$ becomes $0 = dU + PdV$, or $dU = -PdV$.
2. **Internal Energy of an Ideal Gas:** For an ideal gas, the change in internal energy is related to the change in temperature by $dU = C_V dT$, where $C_V$ is the molar specific heat at constant volume.
3. **Differential Ideal Gas Law (for 1 mole):** Differentiating $PV = RT$ yields $P\,dV + V\,dP = R\,dT$.
4. **Mayer's Relation:** This relates the molar specific heats at constant pressure ($C_P$) and constant volume ($C_V$): $R = C_P - C_V$.
5. **Ratio of Specific Heats:** Defined as $\gamma \equiv C_P/C_V$.
From the adiabatic First Law and the internal energy relation, we have $C_V dT = -PdV$.
Substituting $R = C_P - C_V$ into the differential ideal gas law gives $(C_P - C_V)dT = VdP + PdV$.
Now, substitute $PdV = -C_V dT$ into this equation:
$(C_P - C_V)dT = VdP - C_V dT$
The $-C_V dT$ terms on both sides cancel, leading to a second key relation: $C_P dT = VdP$.
We now have two expressions for $dT$:
$dT = -\frac{P\,dV}{C_V}$ and $dT = \frac{V\,dP}{C_P}$.
Equating these gives:
$-\frac{P\,dV}{C_V} = \frac{V\,dP}{C_P}$
Rearranging and introducing $\gamma = C_P/C_V$:
$\frac{C_P}{C_V} = -\frac{V}{P}\frac{dP}{dV}$
$\gamma = -\frac{V}{P}\frac{dP}{dV}$
To solve this, we separate the variables:
$\gamma \frac{dV}{V} = -\frac{dP}{P}$
Integrating both sides from an initial state $(P_1, V_1)$ to a final state $(P_2, V_2)$:
$\int_{V_1}^{V_2} \gamma \frac{dV}{V} = -\int_{P_1}^{P_2} \frac{dP}{P}$
$\gamma \left[ \ln(V) \right]_{V_1}^{V_2} = - \left[ \ln(P) \right]_{P_1}^{P_2}$
$\gamma \ln\left(\frac{V_2}{V_1}\right) = - \ln\left(\frac{P_2}{P_1}\right)$
Using logarithm properties ($\alpha \ln x = \ln x^\alpha$ and $-\ln x = \ln(1/x)$):
$\ln\left(\left(\frac{V_2}{V_1}\right)^\gamma\right) = \ln\left(\frac{P_1}{P_2}\right)$
Exponentiating both sides yields the reversible adiabatic relation:
$P_1 V_1^\gamma = P_2 V_2^\gamma = \text{constant}$
The value of $\gamma$ depends on the type of gas. For monatomic ideal gases, $\gamma = 5/3 \approx 1.67$. For diatomic ideal gases (like air at room temperature), $\gamma = 7/5 = 1.4$.
### 7) Temperature-volume relation for adiabatic processes

From the derived adiabatic relation $PV^\gamma = \text{constant}$ and the ideal gas law $P = \frac{RT}{V}$ (for one mole), a direct relationship between temperature and volume can be obtained.
Substitute $P = \frac{RT}{V}$ into the adiabatic equation:
$\left(\frac{RT}{V}\right) V^\gamma = \text{constant}$
$RT V^{\gamma-1} = \text{constant}$
Since $R$ is a constant, this implies that $T V^{\gamma-1} = \text{constant}$ for a reversible adiabatic process.
This relation can be written in terms of initial and final states as:
$T_1 V_1^{\gamma-1} = T_2 V_2^{\gamma-1}$
or, more practically for calculations:
$T_2 = T_1 \left(\frac{V_1}{V_2}\right)^{\gamma-1}$
This formula is particularly useful for quickly estimating the temperature change during adiabatic compression or expansion, as the exponent $\gamma-1$ directly controls the magnitude of the temperature rise or fall.
### 8) Application: adiabatic compression in the diesel engine (+ live demo)

The principle of adiabatic compression is fundamental to the operation of a diesel engine. In a diesel engine, air is rapidly compressed to a very high temperature. This significant temperature increase is sufficient to ignite the injected fuel without the need for a spark plug.
Consider an estimate for air, which is primarily a diatomic gas, so $\gamma \approx 1.4$. If air starts at room temperature ($T_1 \approx 300\,\text{K}$) and is compressed to one-tenth of its original volume ($V_1/V_2 = 10$), the final temperature $T_2$ can be calculated using the relation $T_2 = T_1 (V_1/V_2)^{\gamma-1}$:
$T_2 = 300\,\text{K} \times (10)^{(1.4 - 1)} = 300\,\text{K} \times 10^{0.4}$
$T_2 \approx 300\,\text{K} \times 2.51 \approx 753\,\text{K}$
This temperature, approximately $480\,^\circ\text{C}$, is ample to ignite diesel fuel. Real diesel engines often have higher compression ratios, sometimes up to $16:1$, leading to even greater final temperatures.
This phenomenon can be dramatically demonstrated with a "fire piston". The setup involves a transparent cylinder containing air and a small piece of cotton wool. When the piston is very rapidly compressed, the air inside heats sufficiently to ignite the cotton wool, which flashes brightly. The "very rapid" compression approximates an adiabatic process, providing visual proof of the substantial temperature rise.
### 9) Introduction to enthalpy: H = U + PV

Enthalpy, denoted by $H$, is a thermodynamic state function defined as $H \equiv U + PV$, where $U$ is the internal energy, $P$ is the pressure, and $V$ is the volume of the system. Since $U$, $P$, and $V$ are all state functions, $H$ is also a state function, meaning its value depends only on the current state of the system, not the path taken to reach that state.
Enthalpy is particularly useful for analysing processes that occur at constant pressure. In such a process, the change in enthalpy, $\Delta H$, is equal to the heat $Q$ transferred into or out of the system. This makes enthalpy a convenient quantity for linking a measurable heat transfer to a state function, especially in open systems or flow processes where volume changes occur against a constant external pressure (e.g., chemical reactions in open containers or continuous flow systems). Enthalpy will be extensively used in the study of the Second Law of Thermodynamics and the analysis of various thermodynamic cycles.
## Key takeaways
Reversibility is an idealised concept for thermodynamic processes where the system remains in quasi-static equilibrium and responds to infinitesimal changes. Such processes extract the maximum useful work and leave the total entropy of the universe unchanged, in contrast to everyday irreversible processes which always increase total entropy.
For gases, the infinitesimal work done *by* the gas is $dW_{\text{by}} = P\,dV$, while the work done *on* the gas is $dW_{\text{on}} = -P\,dV$. The area under the $P-V$ curve represents the magnitude of the work. For an ideal gas undergoing an isothermal expansion and compression along the same path, the net work is zero. When friction is present, the compression and expansion paths diverge, forming a loop on the $P-V$ diagram whose enclosed area represents work lost as heat due to irreversibility.
Adiabatic processes are characterised by no heat exchange ($dQ = 0$). For an ideal gas undergoing a reversible adiabatic process, two key relations hold: $P V^\gamma = \text{constant}$ and $T V^{\gamma-1} = \text{constant}$, where $\gamma = C_P/C_V$ is the ratio of specific heats. For diatomic gases like air at room temperature, $\gamma \approx 1.4$.
A practical application of adiabatic compression is the diesel engine, where rapid compression of air raises its temperature sufficiently to ignite fuel without a spark. For instance, a $10$-fold volume reduction from $300\,\text{K}$ results in a temperature of approximately $750\,\text{K}$ (about $480\,^\circ\text{C}$).
Enthalpy, $H = U + PV$, is a state function that is particularly useful for processes occurring at constant pressure, where the change in enthalpy, $\Delta H$, directly equals the heat $Q$ transferred. This provides a measurable link to a state function, which is valuable in the analysis of thermodynamic cycles and in the context of the Second Law.










