Lecture 11: Heat Engines and the Second Law (Part 1)
0) Orientation and learning outcomes

This lecture builds directly on previous discussions from Lectures 7-10, particularly the First Law of Thermodynamics, including the definitions of internal energy $U$, heat $Q$, and work $W$, along with their sign conventions. We'll also revisit reversible and irreversible processes, $P-V$ work, and adiabatic relations like $PV^\gamma = \text{constant}$ and $TV^{\gamma-1} = \text{constant}$, as demonstrated by the diesel "fire piston" experiment.
Today, we'll shift our focus from simple heat flow to the concept of heat engines. We'll define efficiency and the coefficient of performance (CoP), construct the ideal Carnot cycle to understand its maximum efficiency, and introduce the Second Law of Thermodynamics, along with the formal definition of entropy $S$.
By the end of this lecture, you should be able to determine energy changes for each stage of a given heat-engine cycle, calculate the useful work extracted from a cycle using a $P-V$ diagram, recall and state the Kelvin and Clausius forms of the Second Law, and define entropy, explaining the relationship $dS = dQ_{\text{rev}} / T$.
1) First Law recap and sign conventions
The internal energy $U$ of a system is a state function; its value depends only on the current state of the system (e.g., its temperature and volume), not on how that state was reached. In contrast, heat $Q$ and work $W$ are not state functions but rather processes-they describe the transfer of energy. The First Law of Thermodynamics, essentially a statement of energy conservation, is expressed as:
$$
\Delta U = Q + W
$$
In this formulation, $W$ is positive for work done on the system (e.g., a gas being compressed), and $Q$ is positive when heat enters the system. This convention is consistent with the differential form $dQ = dU + PdV$ where $PdV$ represents work done by the gas. Think of internal energy as a bank account balance: $Q$ and $W$ are deposits or withdrawals that change the balance, but the balance itself ($U$) doesn't care how the money got there, only how much is currently in it. Heat represents energy transfer due to a temperature difference, driven by the chaotic, random motion of particles. Work, on the other hand, is energy transfer accomplished through the ordered, collective motion of particles, such as a piston exerting a force on a gas.
2) From “useless” heat flow to a heat engine
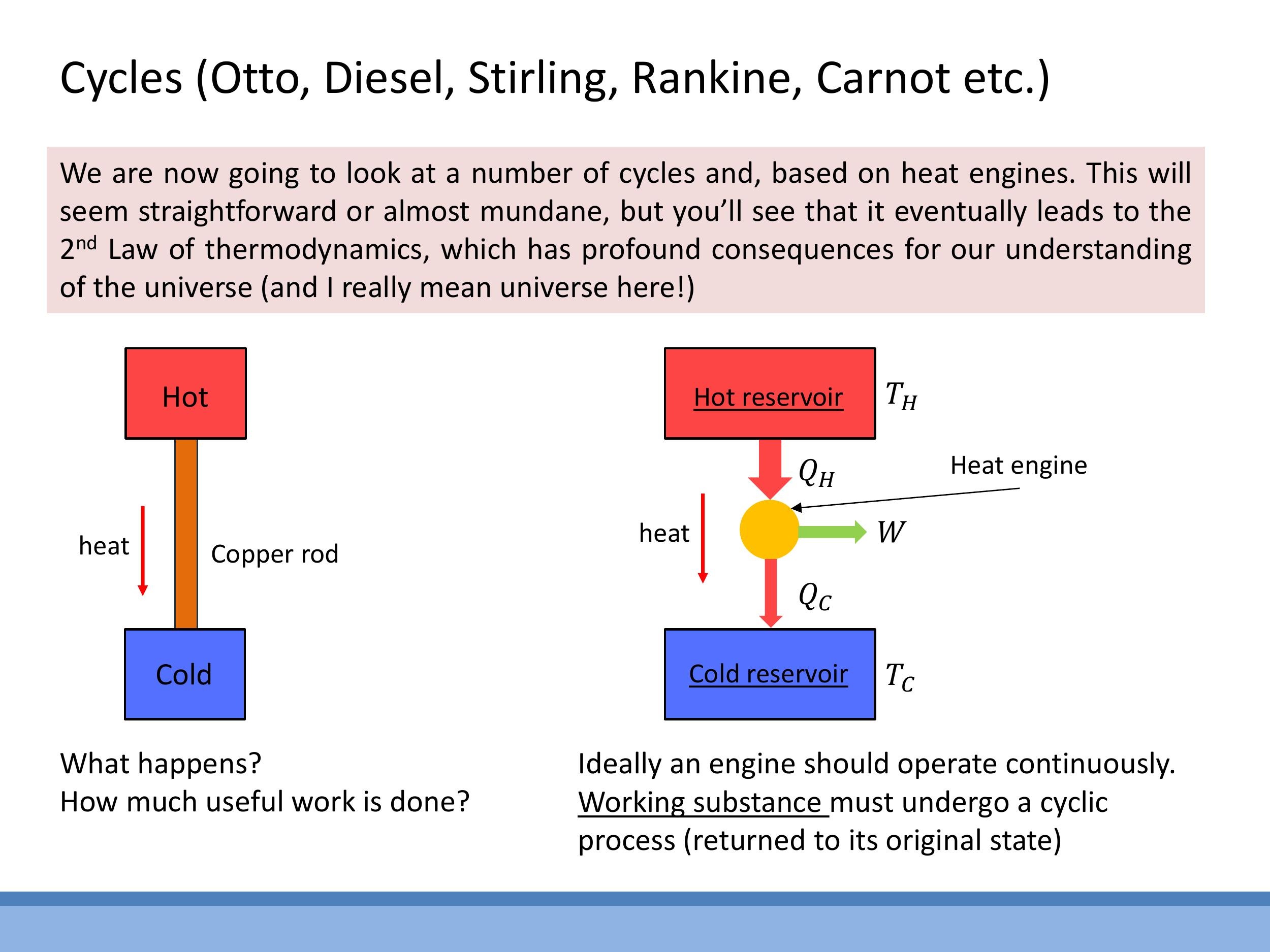
Consider a simple scenario where a hot object and a cold object are connected by a copper rod. Heat will naturally flow from the hot object to the cold object due to the temperature difference. However, this process yields no useful work. To extract useful work from a temperature difference, we need a heat engine.
A heat engine is a device that operates between a high-temperature reservoir (at $T_H$) and a low-temperature reservoir (at $T_C$). It takes in heat $Q_H$ from the hot reservoir, converts some of that energy into useful work $W$, and rejects the remaining heat $Q_C$ to the cold reservoir. For the engine to operate continuously, its working substance (e.g., a gas or steam) must undergo a cyclic process, returning to its initial state after each cycle. This ensures that the internal energy change over a complete cycle is zero ($\Delta U = 0$).
For a complete cycle, according to the First Law ($\Delta U = Q + W$), the net work done by the engine must equal the net heat absorbed. If the engine does work ($W_{\text{out}}$), then $W = -W_{\text{out}}$. If heat $Q_H$ is absorbed and $Q_C$ is rejected, the net heat absorbed is $Q_H - Q_C$. Therefore, the useful work output is:
$$
W = Q_H - Q_C
$$
3) Efficiency of a heat engine
The efficiency, $\varepsilon$, of a heat engine quantifies how effectively it converts the absorbed heat energy into useful work. It's defined as the ratio of the useful work output to the total heat energy input from the hot reservoir:
$$
\varepsilon = \frac{\text{Work out}}{\text{Heat in}} = \frac{W}{Q_H}
$$
Substituting the expression for $W$ from the First Law, we can write the efficiency as:
$$
\varepsilon = \frac{Q_H - Q_C}{Q_H} = 1 - \frac{Q_C}{Q_H}
$$
From this definition, it's clear that the efficiency must always be less than 1 (or 100%). This is because some heat ($Q_C$) must always be rejected to the cold sink to complete a thermodynamic cycle and allow for continuous operation. A heat engine cannot convert all the input heat into work.
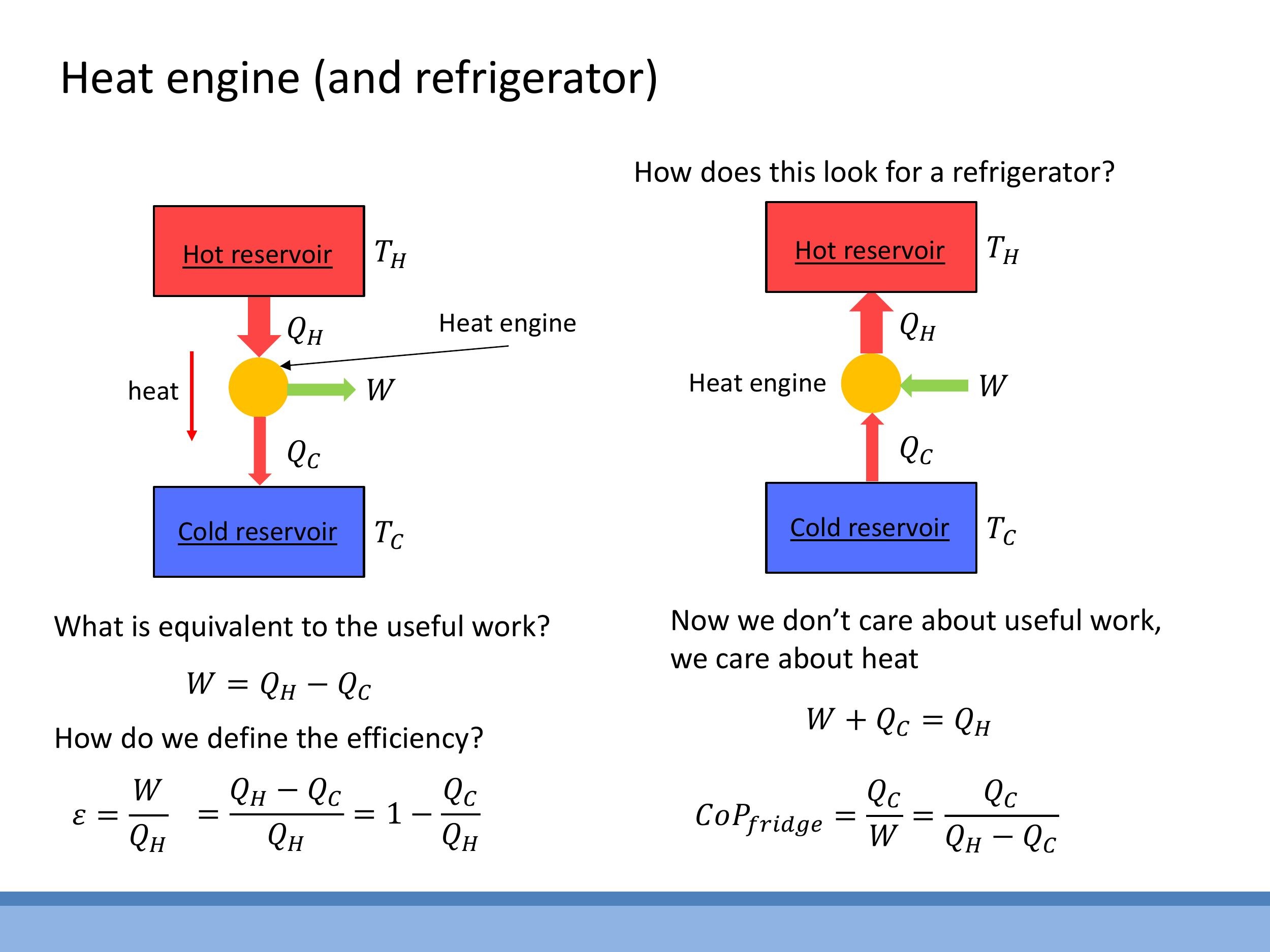
4) Refrigerators and heat pumps (engines run in reverse)

If a heat engine is run in reverse, it functions as a refrigerator or a heat pump. In this mode, external work $W$ is done on the system to transfer heat from a cold reservoir to a hot reservoir-a process that would not occur spontaneously. Specifically, a refrigerator removes heat $Q_C$ from the cold reservoir (e.g., the inside of your fridge) and dumps a larger amount of heat $Q_H$ into the hot reservoir (e.g., the warmer room air behind the fridge). The energy balance for this reversed cycle is:
$$
Q_H = W + Q_C
$$
The performance of a refrigerator or heat pump is not measured by efficiency, but by a coefficient of performance (CoP), which is the ratio of the desired heat transfer to the work input. For a refrigerator, the goal is to remove heat from the cold reservoir, so its CoP is:
$$
\text{CoP}_{\text{fridge}} = \frac{Q_C}{W} = \frac{Q_C}{Q_H - Q_C}
$$
Unlike efficiency, the CoP can be greater than 1. For example, a typical heat pump can achieve a CoP of 3-5, meaning for every unit of electrical work input, 3 to 5 units of heat energy are moved from the cold side to the hot side.
5) The Carnot cycle: the ideal reversible heat engine
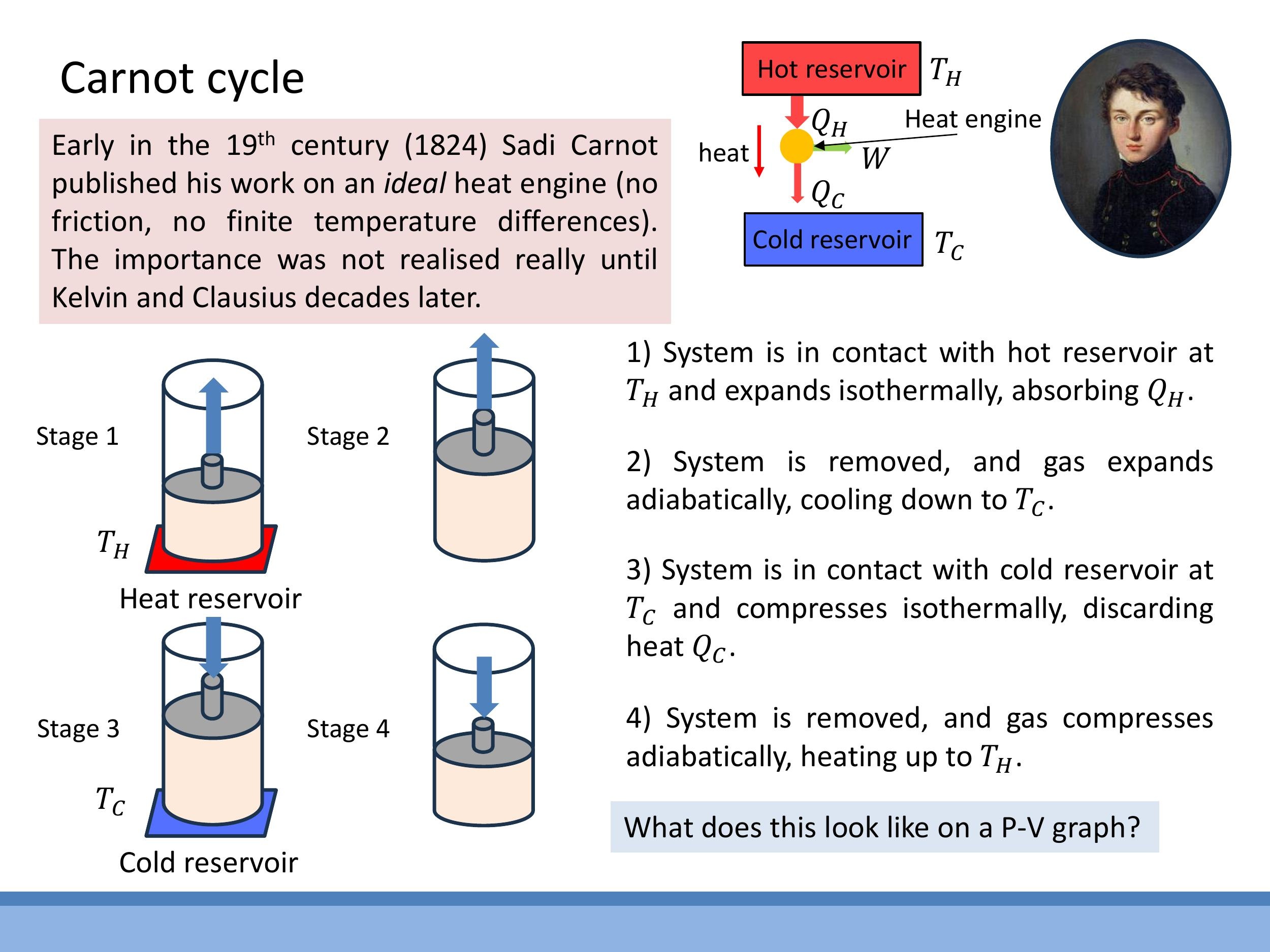
To extract net useful work from an engine, the working substance must undergo a cyclic process that encloses an area on a $P-V$ diagram. A simple back-and-forth along a single isotherm would yield no net work. The Carnot cycle, conceived by Sadi Carnot in 1824, represents the most efficient possible heat engine operating between two given temperatures because it consists entirely of reversible processes.
The Carnot cycle comprises four reversible stages:
- Isothermal Expansion (a $\rightarrow$ b): The working substance absorbs heat $Q_H$ from a hot reservoir at a constant temperature $T_H$. Since the temperature is constant, the change in internal energy $\Delta U$ is zero, meaning all the absorbed heat is converted into work done by the gas.
- Adiabatic Expansion (b $\rightarrow$ c): The system is thermally isolated, so no heat is exchanged ($Q=0$). The gas continues to expand, doing work and causing its temperature to drop from $T_H$ to $T_C$.
- Isothermal Compression (c $\rightarrow$ d): The gas is compressed at a constant cold temperature $T_C$, rejecting heat $Q_C$ to the cold reservoir.
- Adiabatic Compression (d $\rightarrow$ a): The system is again thermally isolated ($Q=0$). Work is done on the gas, increasing its internal energy and raising its temperature back to $T_H$, returning the system to its initial state.
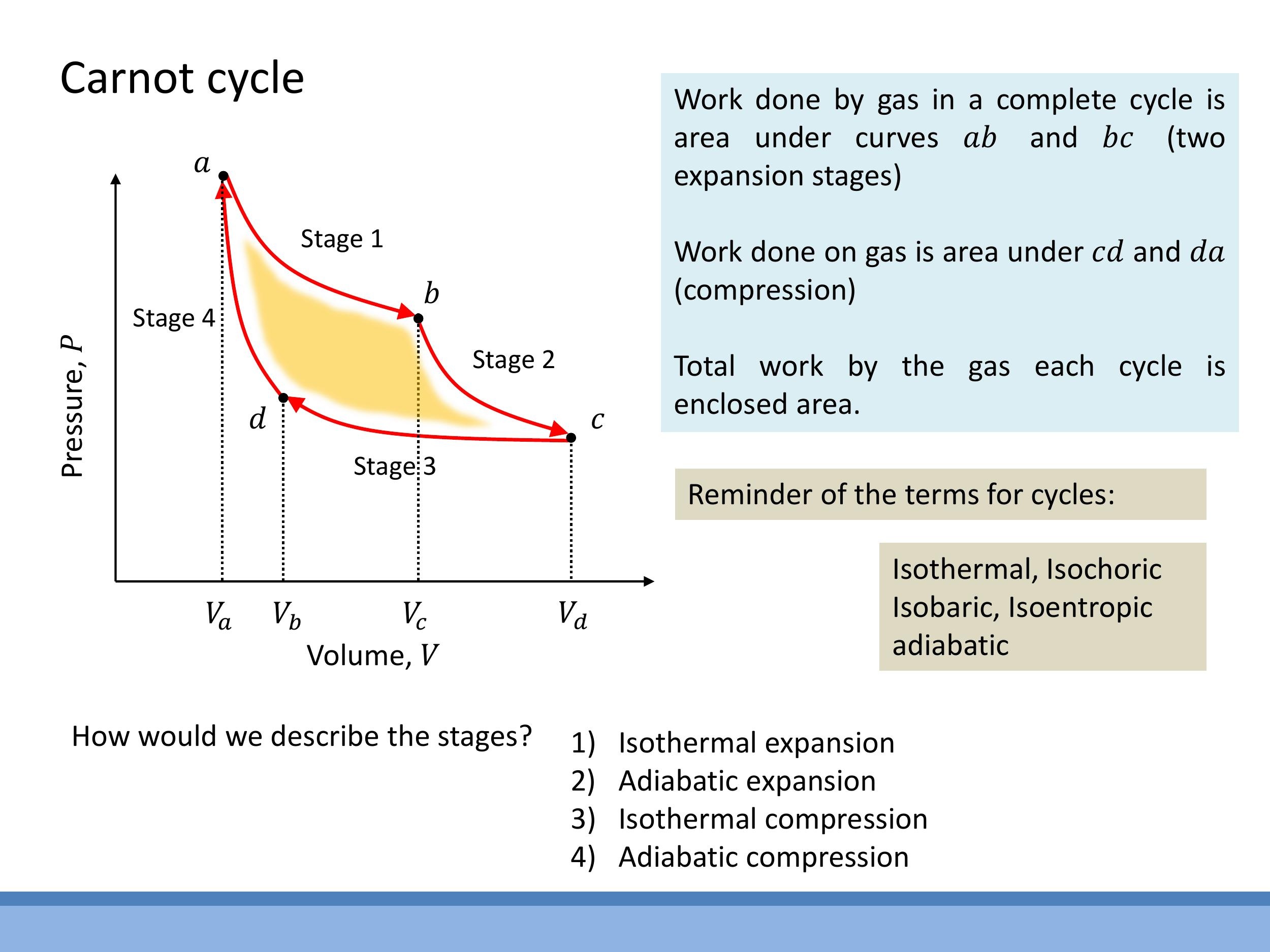
The net work done by the engine during one cycle is represented by the yellow-shaded area enclosed by the loop on the $P-V$ diagram.
To clarify terminology, remember:
- Isothermal means constant temperature.
- Adiabatic means no heat exchange ($Q=0$).
- Isochoric means constant volume.
- Isobaric means constant pressure.
6) Deriving the Carnot efficiency $\varepsilon = 1 - T_C/T_H$
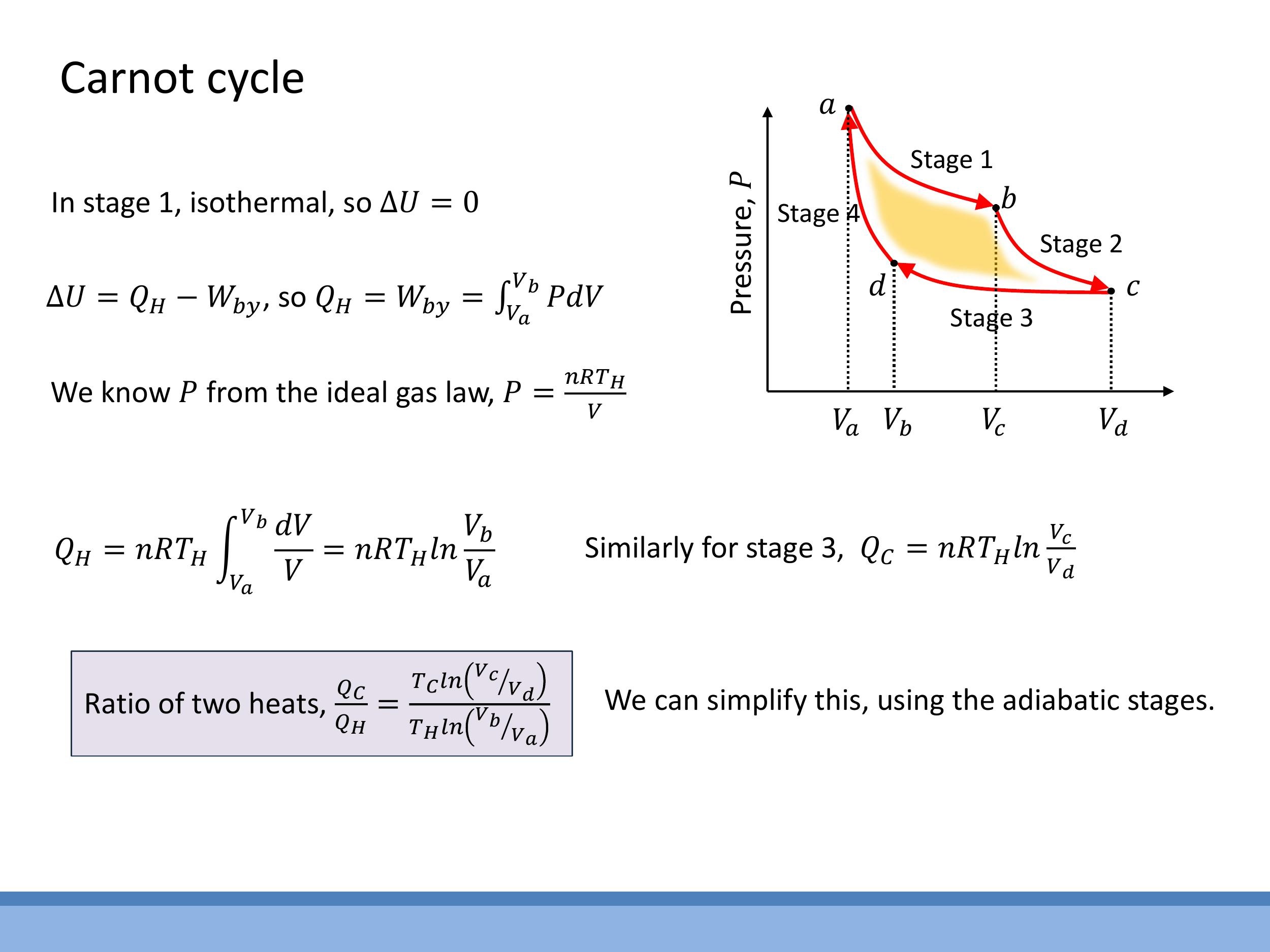
The efficiency of the Carnot engine can be derived by considering the heat exchanges during the isothermal stages and the relationships between volumes during the adiabatic stages.
For the isothermal expansion at $T_H$ (stage 1, a $\rightarrow$ b), where $\Delta U = 0$, the heat absorbed $Q_H$ is equal to the work done by the gas:
$$
Q_H = \int_{V_a}^{V_b} P\,dV
$$
Using the ideal gas law ($P = nRT_H/V$), this integral becomes:
$$
Q_H = nRT_H \int_{V_a}^{V_b} \frac{dV}{V} = nRT_H \ln\left(\frac{V_b}{V_a}\right)
$$
Similarly, for the isothermal compression at $T_C$ (stage 3, c $\rightarrow$ d), the heat rejected $Q_C$ is:
$$
Q_C = nRT_C \ln\left(\frac{V_c}{V_d}\right)
$$
The ratio of these heats is:
$$
\frac{Q_C}{Q_H} = \frac{T_C \ln(V_c/V_d)}{T_H \ln(V_b/V_a)}
$$
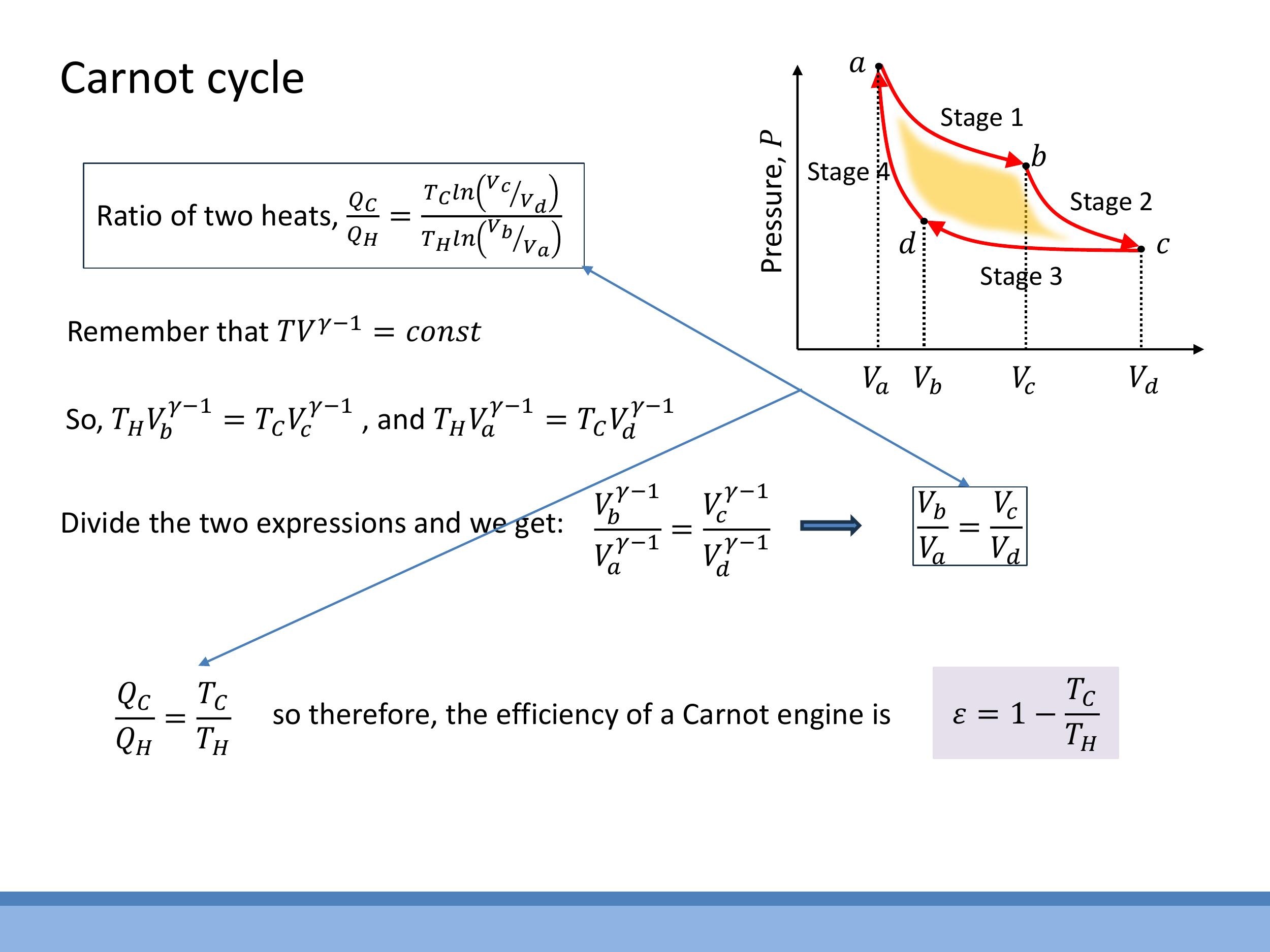
Now, consider the two adiabatic stages (2 and 4). For an adiabatic process, $TV^{\gamma-1} = \text{constant}$.
From stage 2 (b $\rightarrow$ c):
$$
T_H V_b^{\gamma-1} = T_C V_c^{\gamma-1}
$$
From stage 4 (d $\rightarrow$ a):
$$
T_H V_a^{\gamma-1} = T_C V_d^{\gamma-1}
$$
Dividing these two adiabatic relations yields:
$$
\frac{V_b^{\gamma-1}}{V_a^{\gamma-1}} = \frac{V_c^{\gamma-1}}{V_d^{\gamma-1}}
$$
Which simplifies to:
$$
\frac{V_b}{V_a} = \frac{V_c}{V_d}
$$
This crucial result shows that the volume ratios for the two isothermal processes are identical. Substituting this back into the ratio of heats, the logarithm terms cancel:
$$
\frac{Q_C}{Q_H} = \frac{T_C}{T_H}
$$
Finally, substituting this into the general efficiency formula ($\varepsilon = 1 - Q_C/Q_H$), we arrive at the Carnot efficiency:
$$
\varepsilon_{\text{Carnot}} = 1 - \frac{T_C}{T_H}
$$
This formula reveals that the maximum efficiency of a heat engine depends only on the absolute temperatures of the hot and cold reservoirs, and is independent of the working substance or the specific design of the engine. A note on slide labelling: the lecturer indicated a mislabelling of volumes a-d on one of the $P-V$ diagrams, which will be corrected in the uploaded notes.
7) The Stirling cycle and live engine demonstration
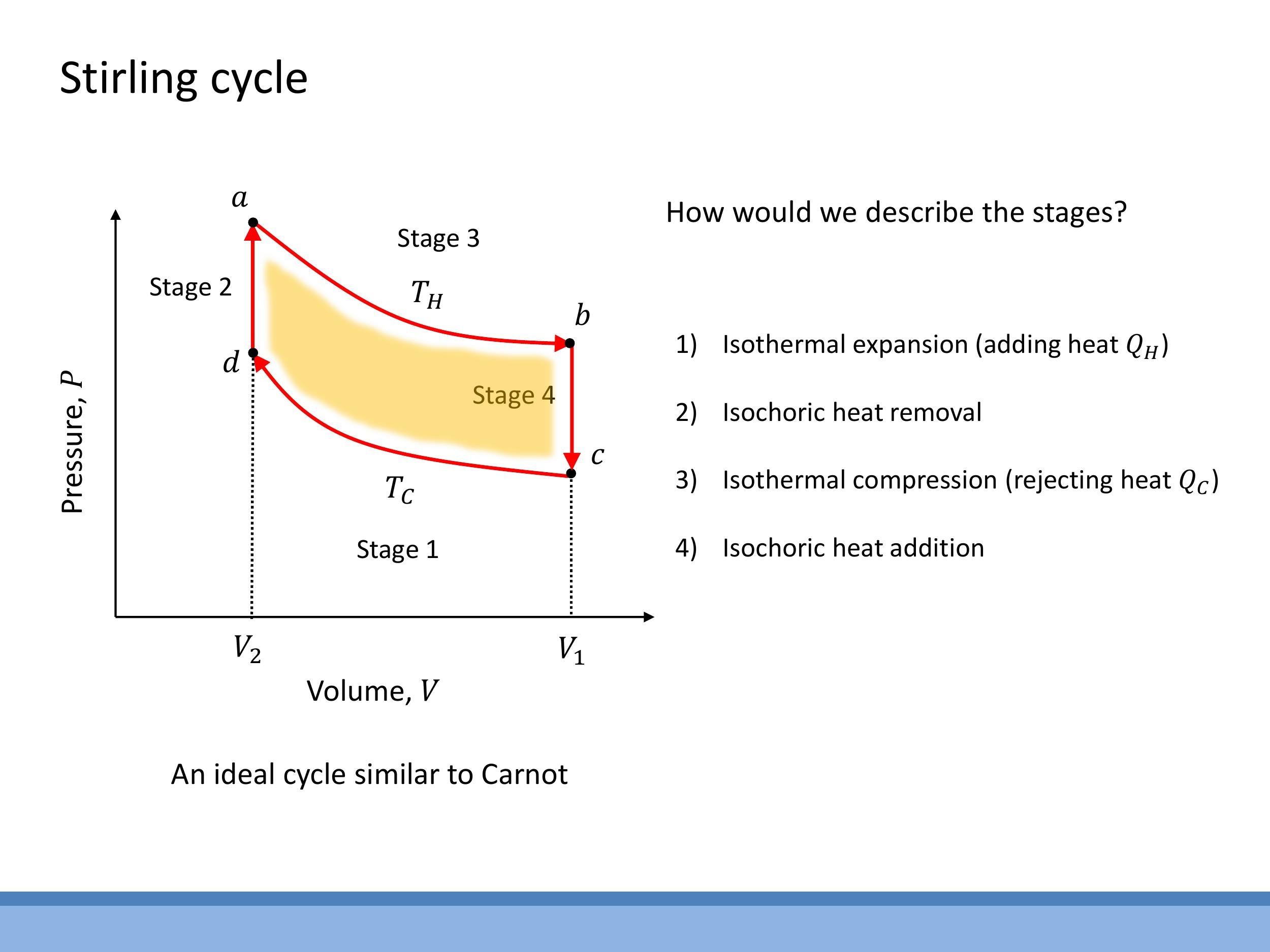
The Stirling cycle is another ideal, reversible heat engine cycle. On a $P-V$ diagram, it consists of two isothermal processes (expansion at $T_H$ and compression at $T_C$) connected by two isochoric (constant volume) processes. When operated reversibly between the same hot and cold reservoir temperatures $T_H$ and $T_C$, an ideal Stirling engine achieves the same maximum efficiency as the Carnot cycle: $\varepsilon = 1 - T_C/T_H$.
To illustrate this dependence, a live demonstration was performed using two Stirling engines. One engine was placed on a hot water bath ($T_H$) with its top plate at room temperature ($T_C$). As the temperature difference established, this engine accelerated rapidly, visually demonstrating that a larger $\Delta T$ leads to stronger performance. A second engine, placed on ice water ($T_C = 0^\circ\text{C}$) with its top plate at room temperature ($T_H$), ran much more slowly, or even struggled to start, reflecting the poorer performance associated with a smaller temperature difference. This speed difference directly reflects the dependence of efficiency on $T_H$ and $T_C$: a larger temperature difference allows for greater available work per cycle.
8) The Second Law: Kelvin and Clausius statements and equivalence

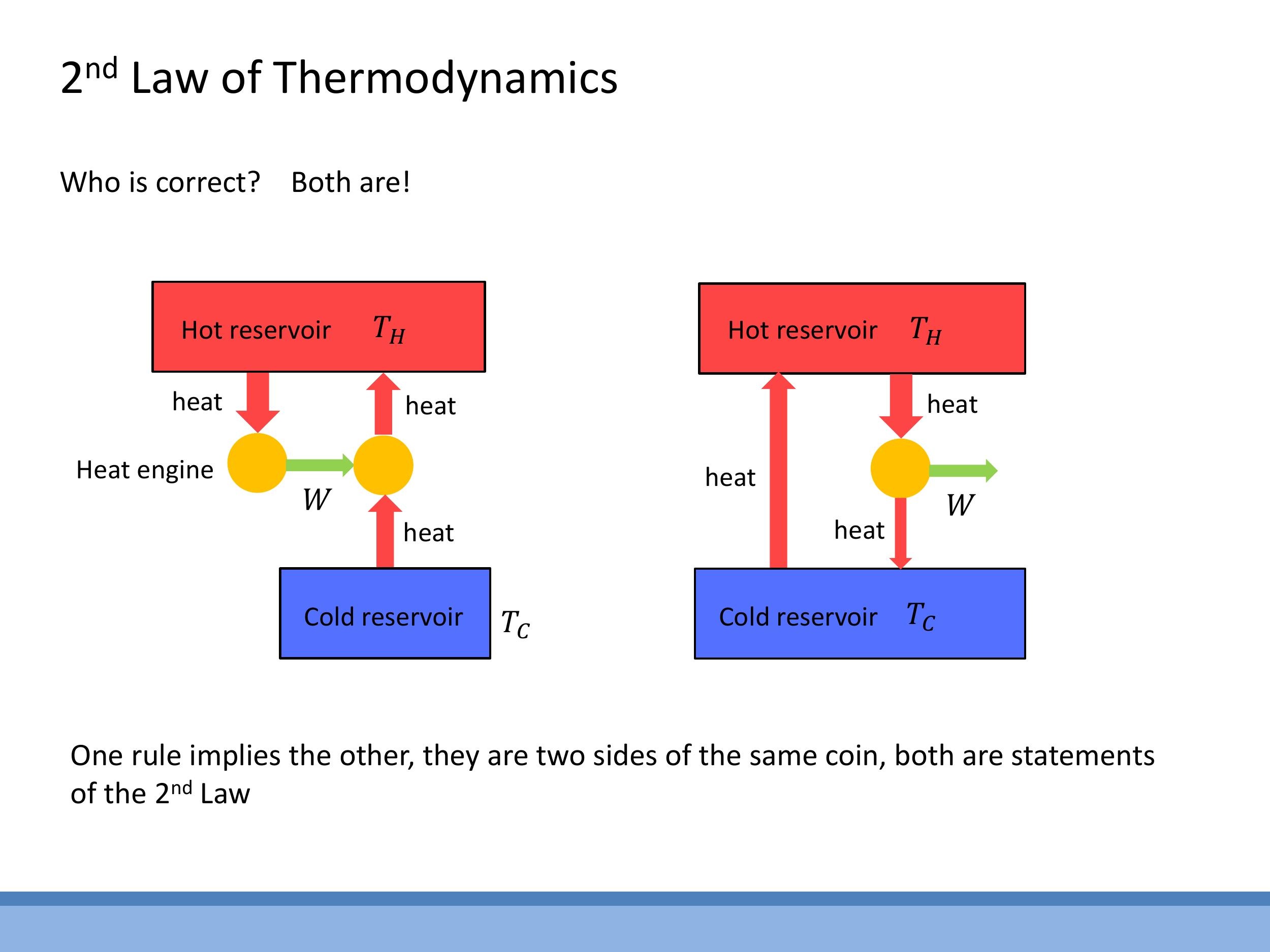
The Second Law of Thermodynamics establishes the direction of spontaneous processes and sets fundamental limits on energy conversion. It can be stated in several equivalent forms, most notably by Clausius and Kelvin.
The Clausius statement asserts that "Heat does not pass from cold to hot spontaneously." This means heat will naturally flow from a region of higher temperature to a region of lower temperature without external intervention. To move heat in the opposite direction (e.g., in a refrigerator), work must be done on the system. Here, "spontaneous" refers to the thermodynamic sense, meaning the process moves towards a more thermodynamically favourable state, regardless of the time it takes.
The Kelvin (Thomson) statement declares that "No cyclic process is possible where heat is taken from a hot source and converted completely to work." This statement highlights the necessity of a cold sink in any practical heat engine cycle. Some energy must always be rejected to a lower-temperature reservoir to complete the cycle and produce net work. A 100% efficient heat engine is therefore impossible.
These two statements are equivalent; if one were false, it would be possible to construct a device that violates the other, demonstrating that they are two fundamental expressions of the same physical law.
9) Entropy: concept and definition

Entropy is a fundamental thermodynamic quantity that measures the degree of disorder or randomness in a system. For instance, a gas typically has higher entropy than a liquid, which in turn has higher entropy than an ordered crystalline solid. Beyond disorder, entropy can also be understood as a measure of the "quality" of energy; high-quality, concentrated energy (like sunlight) is associated with low entropy, while dispersed, low-quality energy (like Earth's infrared emission) is associated with high entropy.
Formally, the change in entropy $dS$ for a reversible process is defined by the reversible heat transferred $dQ_{\text{rev}}$ divided by the absolute thermodynamic temperature $T$ at which the transfer occurs:
$$
dS = \frac{dQ_{\text{rev}}}{T}
$$
The $1/T$ factor in this definition is crucial. As Peter Atkins' analogy suggests, the same amount of heat $dQ$ can have a much larger disordering effect (and thus a larger $dS$) on a cold system (low $T$) than on a hot system (high $T$). Imagine a small sneeze in a quiet library versus at a loud rock concert-the impact on order is vastly different.
A key principle of the Second Law is that the total entropy of the universe (system plus its surroundings) either increases for any real (irreversible) process or remains constant for an ideal (reversible) process. It never decreases. While it is possible to locally decrease entropy and create order (e.g., crystallising a solid), this always requires a larger increase in entropy elsewhere in the surroundings, ensuring that the total entropy of the universe still increases.
10) Consolidation and bridge to next time
The laws of thermodynamics each play a distinct role in our understanding of energy and matter. The Zeroth Law defines temperature, providing a basis for thermal equilibrium. The First Law establishes energy accounting, stating that energy is conserved ($\Delta U = Q + W$), but it doesn't specify the direction of spontaneous processes. The Second Law, however, sets the direction of spontaneous change and imposes ultimate performance bounds on devices like heat engines, encapsulated by the Carnot efficiency.
We now have the foundational concepts for heat engines and refrigerators, including their efficiencies ($\varepsilon$) and coefficients of performance (CoP). We've explored the ideal Carnot cycle, understanding that $\varepsilon_{\text{Carnot}} = 1 - T_C/T_H$ represents the maximum possible efficiency for any engine operating between two temperatures. Furthermore, we've introduced entropy as $dS = dQ_{\text{rev}}/T$, recognising that the total entropy of the universe must increase for real processes.
Next, we'll use these tools to analyse concrete thermodynamic cycles and calculate efficiencies. We'll also begin applying the concept of entropy more extensively to assess the feasibility and reversibility of various processes.
Key takeaways
- Heat flowing directly from hot to cold does no useful work. However, by placing a working substance in a cyclic process between hot and cold reservoirs, we can extract useful work $W = Q_H - Q_C$.
- The efficiency of a heat engine is $\varepsilon = 1 - Q_C/Q_H$. A refrigerator, which is a heat engine run in reverse, has a Coefficient of Performance $\text{CoP} = Q_C/W$, which can exceed 1 because it moves heat rather than creates it.
- The Carnot cycle, composed of two isothermal and two adiabatic reversible stages, is the ideal heat engine. Its efficiency, $\varepsilon_{\text{Carnot}} = 1 - T_C/T_H$, depends solely on the temperatures of the hot and cold reservoirs.
- The Stirling cycle, which uses two isotherms and two isochoric processes, achieves the same ideal efficiency bound as the Carnot cycle when operated reversibly between the same $T_H$ and $T_C$.
- The Second Law of Thermodynamics can be stated in two equivalent forms: Clausius statement: Heat cannot spontaneously flow from a colder body to a hotter body. Kelvin statement: No cyclic device can convert all the heat taken from a single hot source completely into work; a cold sink is essential for continuous operation.
- Entropy $S$ quantifies the dispersal or "quality" of energy. Formally, $dS = dQ_{\text{rev}}/T$. For any real (irreversible) process, the total entropy of the universe (system plus surroundings) increases ($S_{\text{total}} > \text{constant}$), with equality only for perfectly reversible changes.
## Lecture 11: Heat Engines and the Second Law (Part 1)
### 0) Orientation and learning outcomes

This lecture builds directly on previous discussions from Lectures 7-10, particularly the First Law of Thermodynamics, including the definitions of internal energy $U$, heat $Q$, and work $W$, along with their sign conventions. We'll also revisit reversible and irreversible processes, $P-V$ work, and adiabatic relations like $PV^\gamma = \text{constant}$ and $TV^{\gamma-1} = \text{constant}$, as demonstrated by the diesel "fire piston" experiment.
Today, we'll shift our focus from simple heat flow to the concept of heat engines. We'll define efficiency and the coefficient of performance (CoP), construct the ideal Carnot cycle to understand its maximum efficiency, and introduce the Second Law of Thermodynamics, along with the formal definition of entropy $S$.
By the end of this lecture, you should be able to determine energy changes for each stage of a given heat-engine cycle, calculate the useful work extracted from a cycle using a $P-V$ diagram, recall and state the Kelvin and Clausius forms of the Second Law, and define entropy, explaining the relationship $dS = dQ_{\text{rev}} / T$.
### 1) First Law recap and sign conventions
The internal energy $U$ of a system is a state function; its value depends only on the current state of the system (e.g., its temperature and volume), not on how that state was reached. In contrast, heat $Q$ and work $W$ are not state functions but rather processes-they describe the transfer of energy. The First Law of Thermodynamics, essentially a statement of energy conservation, is expressed as:
$$\Delta U = Q + W$$
In this formulation, $W$ is positive for work done *on* the system (e.g., a gas being compressed), and $Q$ is positive when heat *enters* the system. This convention is consistent with the differential form $dQ = dU + PdV$ where $PdV$ represents work done *by* the gas. Think of internal energy as a bank account balance: $Q$ and $W$ are deposits or withdrawals that change the balance, but the balance itself ($U$) doesn't care how the money got there, only how much is currently in it. Heat represents energy transfer due to a temperature difference, driven by the chaotic, random motion of particles. Work, on the other hand, is energy transfer accomplished through the ordered, collective motion of particles, such as a piston exerting a force on a gas.
### 2) From “useless” heat flow to a heat engine

Consider a simple scenario where a hot object and a cold object are connected by a copper rod. Heat will naturally flow from the hot object to the cold object due to the temperature difference. However, this process yields no useful work. To extract useful work from a temperature difference, we need a heat engine.
A heat engine is a device that operates between a high-temperature reservoir (at $T_H$) and a low-temperature reservoir (at $T_C$). It takes in heat $Q_H$ from the hot reservoir, converts some of that energy into useful work $W$, and rejects the remaining heat $Q_C$ to the cold reservoir. For the engine to operate continuously, its working substance (e.g., a gas or steam) must undergo a cyclic process, returning to its initial state after each cycle. This ensures that the internal energy change over a complete cycle is zero ($\Delta U = 0$).
For a complete cycle, according to the First Law ($\Delta U = Q + W$), the net work done by the engine must equal the net heat absorbed. If the engine does work ($W_{\text{out}}$), then $W = -W_{\text{out}}$. If heat $Q_H$ is absorbed and $Q_C$ is rejected, the net heat absorbed is $Q_H - Q_C$. Therefore, the useful work output is:
$$W = Q_H - Q_C$$
### 3) Efficiency of a heat engine

The efficiency, $\varepsilon$, of a heat engine quantifies how effectively it converts the absorbed heat energy into useful work. It's defined as the ratio of the useful work output to the total heat energy input from the hot reservoir:
$$\varepsilon = \frac{\text{Work out}}{\text{Heat in}} = \frac{W}{Q_H}$$
Substituting the expression for $W$ from the First Law, we can write the efficiency as:
$$\varepsilon = \frac{Q_H - Q_C}{Q_H} = 1 - \frac{Q_C}{Q_H}$$
From this definition, it's clear that the efficiency must always be less than 1 (or 100%). This is because some heat ($Q_C$) must always be rejected to the cold sink to complete a thermodynamic cycle and allow for continuous operation. A heat engine cannot convert all the input heat into work.
### 4) Refrigerators and heat pumps (engines run in reverse)

If a heat engine is run in reverse, it functions as a refrigerator or a heat pump. In this mode, external work $W$ is done *on* the system to transfer heat from a cold reservoir to a hot reservoir-a process that would not occur spontaneously. Specifically, a refrigerator removes heat $Q_C$ from the cold reservoir (e.g., the inside of your fridge) and dumps a larger amount of heat $Q_H$ into the hot reservoir (e.g., the warmer room air behind the fridge). The energy balance for this reversed cycle is:
$$Q_H = W + Q_C$$
The performance of a refrigerator or heat pump is not measured by efficiency, but by a coefficient of performance (CoP), which is the ratio of the desired heat transfer to the work input. For a refrigerator, the goal is to remove heat from the cold reservoir, so its CoP is:
$$\text{CoP}_{\text{fridge}} = \frac{Q_C}{W} = \frac{Q_C}{Q_H - Q_C}$$
Unlike efficiency, the CoP can be greater than 1. For example, a typical heat pump can achieve a CoP of 3-5, meaning for every unit of electrical work input, 3 to 5 units of heat energy are moved from the cold side to the hot side.
### 5) The Carnot cycle: the ideal reversible heat engine


To extract net useful work from an engine, the working substance must undergo a cyclic process that encloses an area on a $P-V$ diagram. A simple back-and-forth along a single isotherm would yield no net work. The Carnot cycle, conceived by Sadi Carnot in 1824, represents the most efficient possible heat engine operating between two given temperatures because it consists entirely of reversible processes.
The Carnot cycle comprises four reversible stages:
1. **Isothermal Expansion (a $\rightarrow$ b):** The working substance absorbs heat $Q_H$ from a hot reservoir at a constant temperature $T_H$. Since the temperature is constant, the change in internal energy $\Delta U$ is zero, meaning all the absorbed heat is converted into work done *by* the gas.
2. **Adiabatic Expansion (b $\rightarrow$ c):** The system is thermally isolated, so no heat is exchanged ($Q=0$). The gas continues to expand, doing work and causing its temperature to drop from $T_H$ to $T_C$.
3. **Isothermal Compression (c $\rightarrow$ d):** The gas is compressed at a constant cold temperature $T_C$, rejecting heat $Q_C$ to the cold reservoir.
4. **Adiabatic Compression (d $\rightarrow$ a):** The system is again thermally isolated ($Q=0$). Work is done *on* the gas, increasing its internal energy and raising its temperature back to $T_H$, returning the system to its initial state.
The net work done by the engine during one cycle is represented by the yellow-shaded area enclosed by the loop on the $P-V$ diagram.
To clarify terminology, remember:
* **Isothermal** means constant temperature.
* **Adiabatic** means no heat exchange ($Q=0$).
* **Isochoric** means constant volume.
* **Isobaric** means constant pressure.
### 6) Deriving the Carnot efficiency $\varepsilon = 1 - T_C/T_H$


The efficiency of the Carnot engine can be derived by considering the heat exchanges during the isothermal stages and the relationships between volumes during the adiabatic stages.
For the isothermal expansion at $T_H$ (stage 1, a $\rightarrow$ b), where $\Delta U = 0$, the heat absorbed $Q_H$ is equal to the work done by the gas:
$$Q_H = \int_{V_a}^{V_b} P\,dV$$
Using the ideal gas law ($P = nRT_H/V$), this integral becomes:
$$Q_H = nRT_H \int_{V_a}^{V_b} \frac{dV}{V} = nRT_H \ln\left(\frac{V_b}{V_a}\right)$$
Similarly, for the isothermal compression at $T_C$ (stage 3, c $\rightarrow$ d), the heat rejected $Q_C$ is:
$$Q_C = nRT_C \ln\left(\frac{V_c}{V_d}\right)$$
The ratio of these heats is:
$$\frac{Q_C}{Q_H} = \frac{T_C \ln(V_c/V_d)}{T_H \ln(V_b/V_a)}$$
Now, consider the two adiabatic stages (2 and 4). For an adiabatic process, $TV^{\gamma-1} = \text{constant}$.
From stage 2 (b $\rightarrow$ c):
$$T_H V_b^{\gamma-1} = T_C V_c^{\gamma-1}$$
From stage 4 (d $\rightarrow$ a):
$$T_H V_a^{\gamma-1} = T_C V_d^{\gamma-1}$$
Dividing these two adiabatic relations yields:
$$\frac{V_b^{\gamma-1}}{V_a^{\gamma-1}} = \frac{V_c^{\gamma-1}}{V_d^{\gamma-1}}$$
Which simplifies to:
$$\frac{V_b}{V_a} = \frac{V_c}{V_d}$$
This crucial result shows that the volume ratios for the two isothermal processes are identical. Substituting this back into the ratio of heats, the logarithm terms cancel:
$$\frac{Q_C}{Q_H} = \frac{T_C}{T_H}$$
Finally, substituting this into the general efficiency formula ($\varepsilon = 1 - Q_C/Q_H$), we arrive at the Carnot efficiency:
$$\varepsilon_{\text{Carnot}} = 1 - \frac{T_C}{T_H}$$
This formula reveals that the maximum efficiency of a heat engine depends *only* on the absolute temperatures of the hot and cold reservoirs, and is independent of the working substance or the specific design of the engine. A note on slide labelling: the lecturer indicated a mislabelling of volumes a-d on one of the $P-V$ diagrams, which will be corrected in the uploaded notes.
### 7) The Stirling cycle and live engine demonstration

The Stirling cycle is another ideal, reversible heat engine cycle. On a $P-V$ diagram, it consists of two isothermal processes (expansion at $T_H$ and compression at $T_C$) connected by two isochoric (constant volume) processes. When operated reversibly between the same hot and cold reservoir temperatures $T_H$ and $T_C$, an ideal Stirling engine achieves the same maximum efficiency as the Carnot cycle: $\varepsilon = 1 - T_C/T_H$.
To illustrate this dependence, a live demonstration was performed using two Stirling engines. One engine was placed on a hot water bath ($T_H$) with its top plate at room temperature ($T_C$). As the temperature difference established, this engine accelerated rapidly, visually demonstrating that a larger $\Delta T$ leads to stronger performance. A second engine, placed on ice water ($T_C = 0^\circ\text{C}$) with its top plate at room temperature ($T_H$), ran much more slowly, or even struggled to start, reflecting the poorer performance associated with a smaller temperature difference. This speed difference directly reflects the dependence of efficiency on $T_H$ and $T_C$: a larger temperature difference allows for greater available work per cycle.
### 8) The Second Law: Kelvin and Clausius statements and equivalence


The Second Law of Thermodynamics establishes the direction of spontaneous processes and sets fundamental limits on energy conversion. It can be stated in several equivalent forms, most notably by Clausius and Kelvin.
The **Clausius statement** asserts that "Heat does not pass from cold to hot spontaneously." This means heat will naturally flow from a region of higher temperature to a region of lower temperature without external intervention. To move heat in the opposite direction (e.g., in a refrigerator), work must be done on the system. Here, "spontaneous" refers to the thermodynamic sense, meaning the process moves towards a more thermodynamically favourable state, regardless of the time it takes.
The **Kelvin (Thomson) statement** declares that "No cyclic process is possible where heat is taken from a hot source and converted completely to work." This statement highlights the necessity of a cold sink in any practical heat engine cycle. Some energy must always be rejected to a lower-temperature reservoir to complete the cycle and produce net work. A 100% efficient heat engine is therefore impossible.
These two statements are equivalent; if one were false, it would be possible to construct a device that violates the other, demonstrating that they are two fundamental expressions of the same physical law.
### 9) Entropy: concept and definition

Entropy is a fundamental thermodynamic quantity that measures the degree of disorder or randomness in a system. For instance, a gas typically has higher entropy than a liquid, which in turn has higher entropy than an ordered crystalline solid. Beyond disorder, entropy can also be understood as a measure of the "quality" of energy; high-quality, concentrated energy (like sunlight) is associated with low entropy, while dispersed, low-quality energy (like Earth's infrared emission) is associated with high entropy.
Formally, the change in entropy $dS$ for a reversible process is defined by the reversible heat transferred $dQ_{\text{rev}}$ divided by the absolute thermodynamic temperature $T$ at which the transfer occurs:
$$dS = \frac{dQ_{\text{rev}}}{T}$$
The $1/T$ factor in this definition is crucial. As Peter Atkins' analogy suggests, the same amount of heat $dQ$ can have a much larger disordering effect (and thus a larger $dS$) on a cold system (low $T$) than on a hot system (high $T$). Imagine a small sneeze in a quiet library versus at a loud rock concert-the impact on order is vastly different.
A key principle of the Second Law is that the total entropy of the universe (system plus its surroundings) either increases for any real (irreversible) process or remains constant for an ideal (reversible) process. It never decreases. While it is possible to locally decrease entropy and create order (e.g., crystallising a solid), this always requires a larger increase in entropy elsewhere in the surroundings, ensuring that the total entropy of the universe still increases.
### 10) Consolidation and bridge to next time
The laws of thermodynamics each play a distinct role in our understanding of energy and matter. The Zeroth Law defines temperature, providing a basis for thermal equilibrium. The First Law establishes energy accounting, stating that energy is conserved ($\Delta U = Q + W$), but it doesn't specify the direction of spontaneous processes. The Second Law, however, sets the direction of spontaneous change and imposes ultimate performance bounds on devices like heat engines, encapsulated by the Carnot efficiency.
We now have the foundational concepts for heat engines and refrigerators, including their efficiencies ($\varepsilon$) and coefficients of performance (CoP). We've explored the ideal Carnot cycle, understanding that $\varepsilon_{\text{Carnot}} = 1 - T_C/T_H$ represents the maximum possible efficiency for any engine operating between two temperatures. Furthermore, we've introduced entropy as $dS = dQ_{\text{rev}}/T$, recognising that the total entropy of the universe must increase for real processes.
Next, we'll use these tools to analyse concrete thermodynamic cycles and calculate efficiencies. We'll also begin applying the concept of entropy more extensively to assess the feasibility and reversibility of various processes.
## Key takeaways
* Heat flowing directly from hot to cold does no useful work. However, by placing a working substance in a cyclic process between hot and cold reservoirs, we can extract useful work $W = Q_H - Q_C$.
* The efficiency of a heat engine is $\varepsilon = 1 - Q_C/Q_H$. A refrigerator, which is a heat engine run in reverse, has a Coefficient of Performance $\text{CoP} = Q_C/W$, which can exceed 1 because it moves heat rather than creates it.
* The Carnot cycle, composed of two isothermal and two adiabatic reversible stages, is the ideal heat engine. Its efficiency, $\varepsilon_{\text{Carnot}} = 1 - T_C/T_H$, depends solely on the temperatures of the hot and cold reservoirs.
* The Stirling cycle, which uses two isotherms and two isochoric processes, achieves the same ideal efficiency bound as the Carnot cycle when operated reversibly between the same $T_H$ and $T_C$.
* The Second Law of Thermodynamics can be stated in two equivalent forms:
* **Clausius statement:** Heat cannot spontaneously flow from a colder body to a hotter body.
* **Kelvin statement:** No cyclic device can convert all the heat taken from a single hot source completely into work; a cold sink is essential for continuous operation.
* Entropy $S$ quantifies the dispersal or "quality" of energy. Formally, $dS = dQ_{\text{rev}}/T$. For any real (irreversible) process, the total entropy of the universe (system plus surroundings) increases ($S_{\text{total}} > \text{constant}$), with equality only for perfectly reversible changes.











