Lecture 12: Heat Engines and the Second Law (part 2)
This lecture builds on the concepts of heat engines, cycles on P-V diagrams, reversible and irreversible processes, and adiabats that we discussed previously. Today, we'll formalise the Second Law of Thermodynamics through the Kelvin and Clausius statements. We'll then introduce entropy ($S$) as a crucial new state function, explore T-S diagrams, and learn how to perform practical entropy calculations for simple thermodynamic processes.
Our learning outcomes for this session are to recall the Second Law and understand the equivalence between the Kelvin and Clausius statements. You'll also learn to connect entropy to heat transfer and temperature using the definition $\mathrm{d}S = \mathrm{d}Q_{\text{rev}}/T$. We'll practise transforming a Carnot cycle between P-V and T-S descriptions, and finally, you'll be able to calculate entropy changes in various simple, representative processes, both reversible and irreversible.

1) Useful work needs a cycle: the Carnot picture (quick recap)
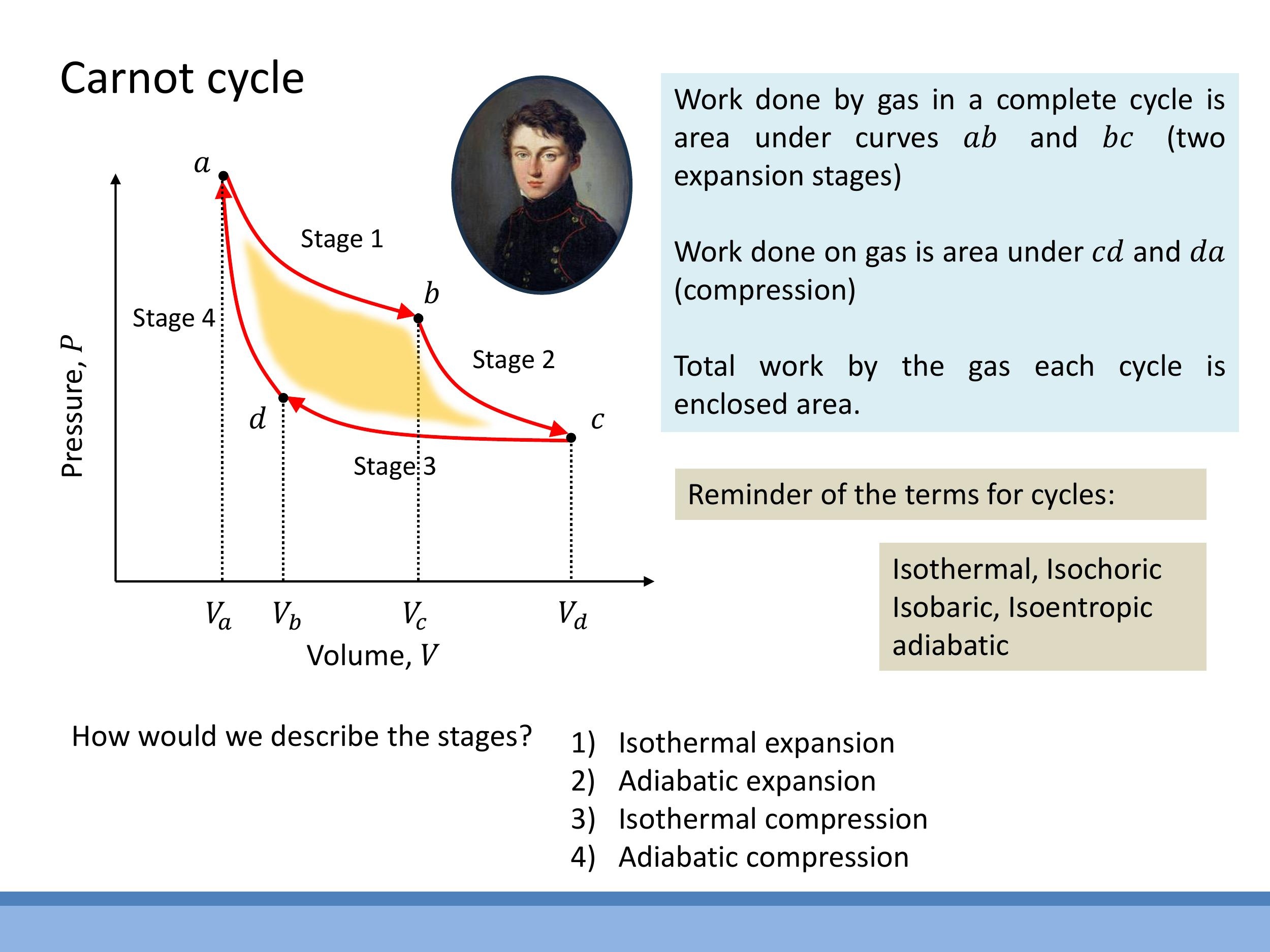
To perform useful work repeatedly, a working substance must operate in a cycle, meaning it returns to its initial state after each sequence of operations. This cyclical process is typically visualised on a P-V diagram, where the net work done by the system is represented by the area enclosed by the cycle's path.
The Carnot cycle, an idealised and perfectly reversible heat engine, consists of four distinct stages:
- Isothermal expansion at $T_H$: The working substance absorbs heat $Q_H$ from a hot reservoir while expanding at a constant high temperature $T_H$. For an ideal gas undergoing an isothermal process, the change in internal energy $\Delta U$ is zero, so all the absorbed heat is converted into work done by the gas.
- Adiabatic expansion: The system is thermally isolated, meaning no heat is exchanged ($Q=0$). The gas continues to expand, doing work, which causes its temperature to drop from $T_H$ to $T_C$.
- Isothermal compression at $T_C$: The gas is then compressed at a constant low temperature $T_C$, rejecting heat $Q_C$ to a cold reservoir.
- Adiabatic compression: Again, the system is thermally isolated ($Q=0$). Work is done on the gas as it is compressed, increasing its internal energy and raising its temperature back to $T_H$, thus completing the cycle.
From our previous discussion, the efficiency of an ideal Carnot engine is given by $\varepsilon_{\text{Carnot}} = 1 - T_C/T_H$. This formula highlights a fundamental limit: the maximum possible efficiency depends solely on the absolute temperatures of the hot and cold reservoirs, not on the specific working substance. The Stirling cycle, another theoretical ideal engine, replaces the adiabatic legs of the Carnot cycle with isochoric (constant volume) processes but achieves the same maximum efficiency when operating reversibly between the same high and low temperatures, $T_H$ and $T_C$.
2) Vocabulary refresh for processes
As we delve deeper into thermodynamics, it's helpful to refresh our understanding of key terms that describe various processes:
- Isothermal: A process where the temperature ($T$) of the system remains constant.
- Isochoric: A process where the volume ($V$) of the system remains constant.
- Isobaric: A process where the pressure ($P$) of the system remains constant.
- Isentropic: A process where the entropy ($S$) of the system remains constant. This usually implies a reversible adiabatic process.
- Adiabatic: A process where no heat ($Q$) is transferred into or out of the system ($\mathrm{d}Q = 0$).
These definitions are crucial for interpreting thermodynamic diagrams and calculations.
3) The Second Law: Kelvin and Clausius statements and why they’re equivalent
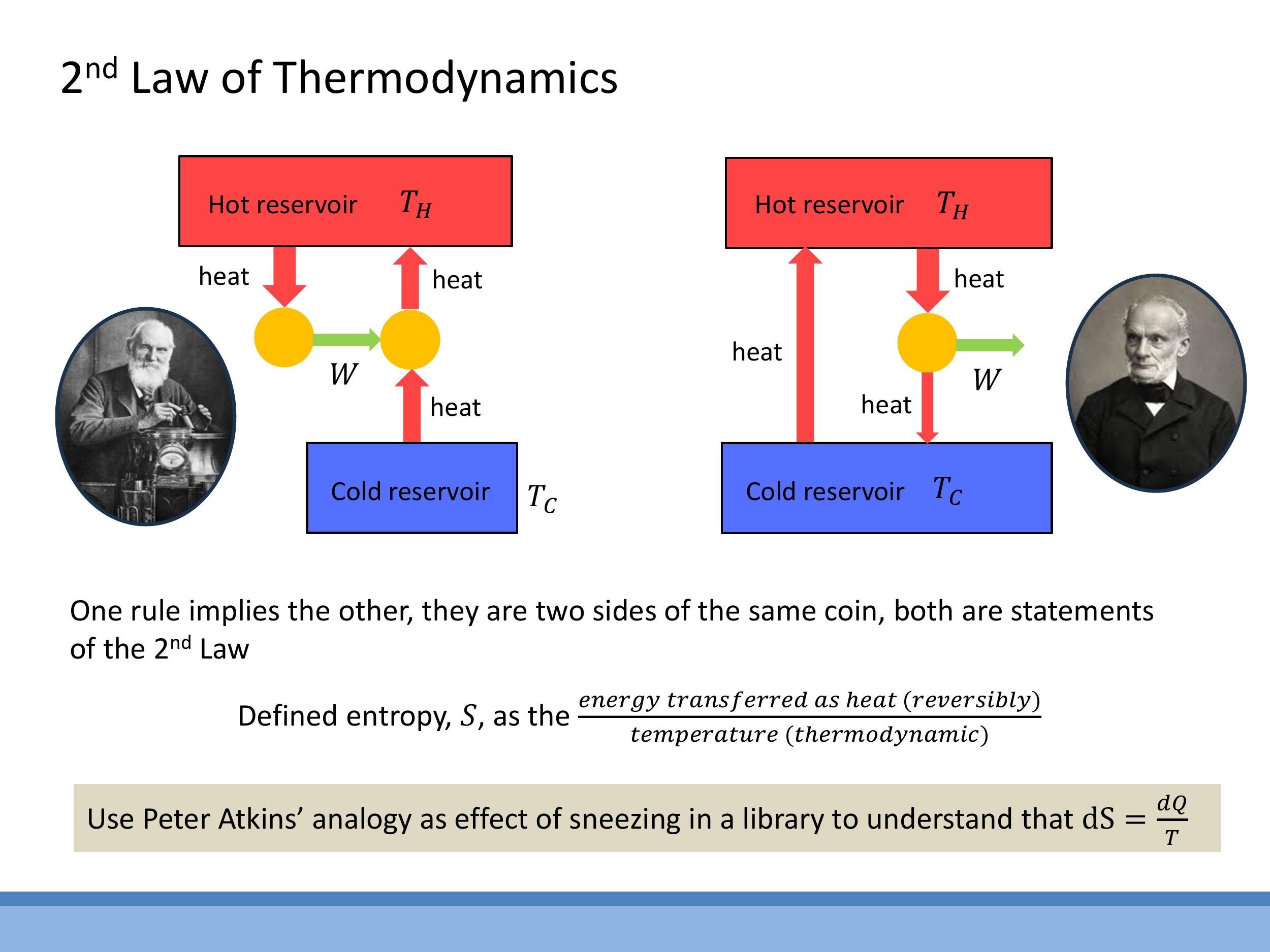
The Second Law of Thermodynamics places fundamental limitations on how energy can be converted and transferred. It has two equivalent formulations, known as the Kelvin (or Kelvin-Planck) statement and the Clausius statement.
The Kelvin statement asserts that it is impossible for any cyclic device to extract heat from a single hot reservoir and convert it entirely into useful work. This means that a cold sink, or a cold reservoir, is always necessary for a heat engine to operate continuously and produce net work. Without a cold sink to dump excess heat, the cycle cannot be completed without violating the Second Law.
The Clausius statement declares that heat does not spontaneously flow from a colder body to a hotter body. This aligns with our everyday experience: a hot cup of coffee cools down in a room, but a cold drink doesn't spontaneously get hotter by absorbing heat from the cooler room. To move heat "uphill," from a cold region to a hot region (as in a refrigerator or heat pump), external work must be supplied to the system.
These two statements are not independent; they are two sides of the same fundamental law. If one statement were false, it would be possible to construct a hypothetical device that violates the other. For instance, if the Kelvin statement were false, we could build an engine that converts all heat into work. We could then use some of that work to drive a refrigerator (which is a device that moves heat from cold to hot) in such a way that it violates the Clausius statement. Similarly, if the Clausius statement were false, we could create a device that spontaneously moves heat from cold to hot, and by combining it with an engine, we could violate the Kelvin statement. Thus, their equivalence means that if one is true, the other must also be true, and vice-versa.

4) Entropy $S$: what it measures and its definitions
Entropy ($S$) is a central concept in thermodynamics, providing a quantitative measure of the "disorder" or "energy spread" within a system. We can think of its physical meaning in several ways:
- Disorder view: This is the most common intuitive picture. A gas, with its randomly moving molecules, has higher entropy than a liquid, which in turn has higher entropy than an ordered crystalline solid. The more disordered a system, the higher its entropy.
- Energy spread view: Entropy can also be understood as a measure of how widely energy is distributed among the accessible microscopic states of a system. In a gas, energy is spread over a vast range of positions and velocities for its molecules, leading to high entropy. In contrast, in a solid, energy is mostly confined to vibrations around fixed positions, resulting in lower entropy.
- Energy quality view: Entropy is inversely related to the "quality" or usability of energy. High-quality, concentrated energy (like sunlight) is considered low-entropy, while dispersed, "waste heat" is high-entropy. Biological processes, for example, increase the entropy of the universe by degrading high-quality energy into more dispersed, lower-quality forms.
The thermodynamic definition of entropy provides a precise mathematical formulation. It states that an infinitesimal change in entropy ($\mathrm{d}S$) is equal to the infinitesimal amount of heat transferred reversibly ($\mathrm{d}Q_{\text{rev}}$) divided by the absolute temperature ($T$) at which the transfer occurs:
$$
\mathrm{d}S = \frac{\mathrm{d}Q_{\text{rev}}}{T}
$$
The $1/T$ factor in this definition is crucial. To build intuition, consider Peter Atkins' analogy: the same "sneeze" (representing an amount of heat $\mathrm{d}Q$) causes a much larger disturbance (a larger $\mathrm{d}S$) in a quiet library (low $T$) than on a bustling street (high $T$). This helps us understand why a given amount of heat has a more significant disordering effect on a colder system.
Side Note: The statistical definition of entropy, formulated by Ludwig Boltzmann, connects entropy to the microscopic world. His famous equation, $S = k \ln W$, relates entropy ($S$) to Boltzmann's constant ($k$) and the natural logarithm of the number of accessible microstates ($W$) for a system. While this provides a deeper understanding of entropy's statistical nature, we won't use it for calculations in this course.

5) The Carnot cycle on a T-S diagram and a simpler route to $\varepsilon$
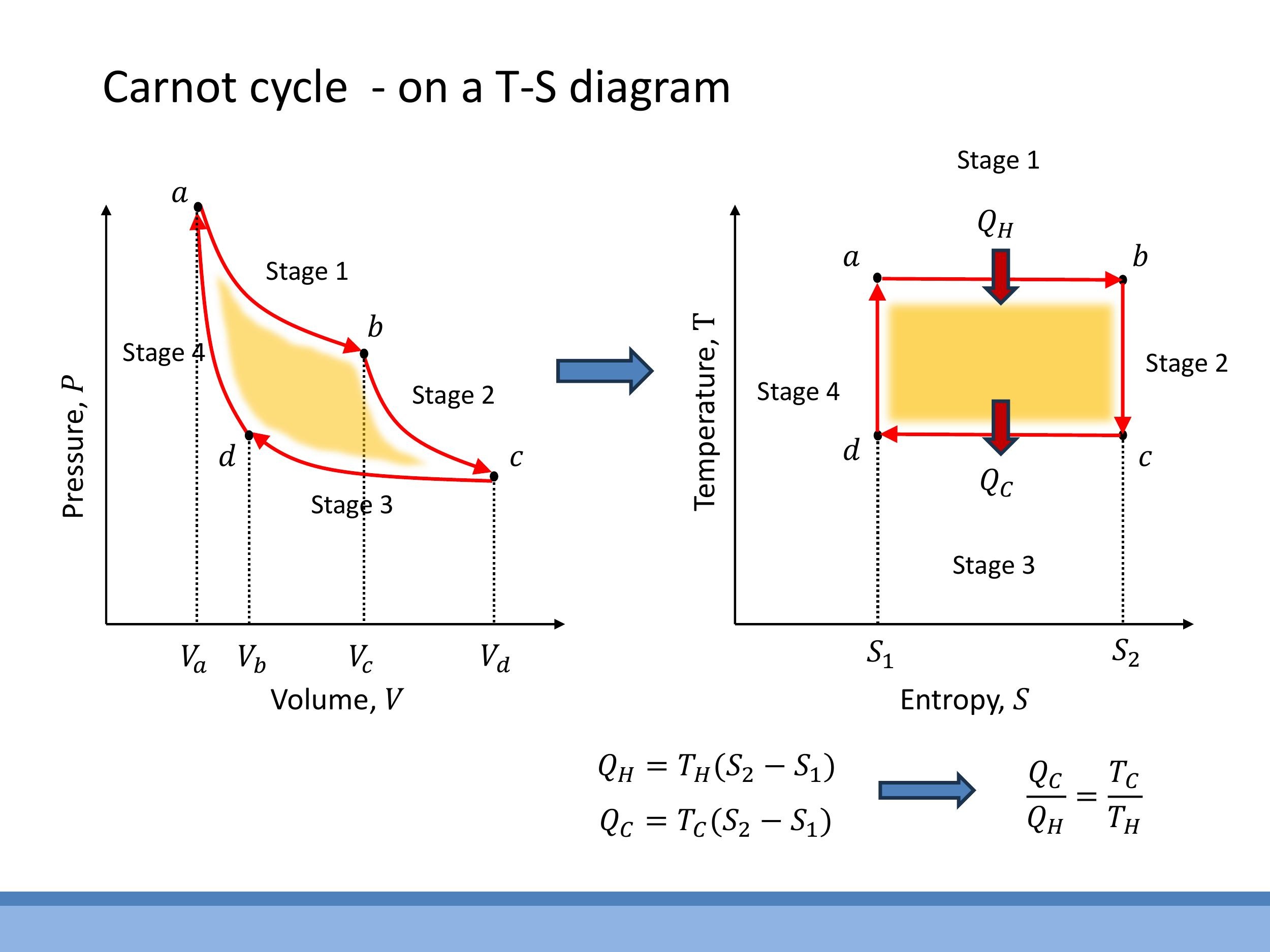
While P-V diagrams are useful for visualising work, Temperature-Entropy (T-S) diagrams offer a powerful alternative, especially for understanding the Carnot cycle and its efficiency.
On a T-S diagram, the four reversible stages of the Carnot cycle transform into a simple rectangle:
- Isothermal expansion (a→b): During this stage, the temperature remains constant at $T_H$, and the entropy of the system increases as the gas expands. This is represented by a horizontal line segment moving from left to right on the T-S diagram.
- Adiabatic expansion (b→c): This is a reversible process with no heat transfer ($\mathrm{d}Q = 0$). Since $\mathrm{d}S = \mathrm{d}Q_{\text{rev}}/T$, the entropy change is zero. As the gas expands, its temperature drops from $T_H$ to $T_C$. This is represented by a vertical line segment moving downwards.
- Isothermal compression (c→d): The temperature remains constant at $T_C$, and the entropy of the system decreases as the gas is compressed. This is a horizontal line segment moving from right to left.
- Adiabatic compression (d→a): Again, there is no heat transfer, so the entropy change is zero. Work is done on the gas, raising its temperature back to $T_H$, completing the cycle with a vertical line segment moving upwards.
The resulting shape on a T-S diagram is a perfect rectangle bounded by the hot temperature $T_H$, the cold temperature $T_C$, and the entropy values $S_1$ and $S_2$.
This T-S representation provides a remarkably straightforward way to derive the Carnot efficiency. On a T-S diagram, the heat transferred during an isothermal process is simply the area under the horizontal line representing that isotherm.
- The heat absorbed from the hot reservoir ($Q_H$) is the area under the top isotherm: $Q_H = T_H \Delta S$, where $\Delta S = S_2 - S_1$.
- The heat rejected to the cold reservoir ($Q_C$) is the area under the bottom isotherm: $Q_C = T_C \Delta S$, where $\Delta S = S_2 - S_1$.
By taking the ratio of these heats, we immediately find $Q_C/Q_H = T_C/T_H$. Substituting this into the general efficiency formula, $\varepsilon = 1 - Q_C/Q_H$, yields the Carnot efficiency: $\varepsilon = 1 - T_C/T_H$. This demonstrates that both the P-V and T-S diagrams describe the same underlying physics, but the T-S diagram offers a more elegant and immediate route to understanding the efficiency, compressing the algebra into simple geometry.
6) Calculating entropy changes: representative worked cases
Entropy is a state function, meaning its change depends only on the initial and final states of a system, not on the path taken. However, when calculating $\Delta S$, we often need to consider a reversible path between those states. Let's look at some examples.
6.1 Reversible phase change at fixed T: melting ice at 0 °C
Consider a small amount of ice melting into water at $0 \, ^\circ\text{C} $ ($ 273.15 \, \text{K}$). This is an idealised reversible process.
- For the ice, which absorbs heat (latent heat of fusion, $L_{\text{fus}}$), the entropy change is $\Delta S_{\text{ice}} = Q/T = mL_{\text{fus}}/T$. If we take $m = 15 \, \text{g} $ ($ 0.015 \, \text{kg} $) and $ L_{\text{fus}} = 334 \, \text{kJ kg}^{-1} $, then $ \Delta S_{\text{ice}} = (0.015 \, \text{kg})(334 \times 10^3 \, \text{J kg}^{-1}) / (273.15 \, \text{K}) \approx +18.3 \, \text{J K}^{-1}$.
- The water (or surroundings) provides this heat, so its entropy change is equal in magnitude but opposite in sign: $\Delta S_{\text{water}} = -18.3 \, \text{J K}^{-1}$.
- For the total isolated and reversible system, the total entropy change is $\Delta S_{\text{total}} = \Delta S_{\text{ice}} + \Delta S_{\text{water}} = 0$. This is an isentropic process. The equal and opposite entropy changes reflect the reversible heat exchange at a fixed temperature.

6.2 Reversible isothermal expansion of an ideal gas
For a reversible isothermal expansion of an ideal gas, the internal energy change $\Delta U = 0$. Therefore, the heat absorbed ($Q$) is equal to the work done by the gas ($W$). The work done during an isothermal expansion of one mole of an ideal gas is $W = \int P \, \mathrm{d}V = RT \ln(V_2/V_1)$.
- Since $Q = W$, the heat absorbed is $Q = RT \ln(V_2/V_1)$.
- The entropy change of the system is $\Delta S_{\text{sys}} = Q/T = R \ln(V_2/V_1)$. Since $V_2 > V_1$, the system's entropy increases.
- For a fully reversible process, the surroundings must experience an equal and opposite entropy change, so $\Delta S_{\text{surr}} = -R \ln(V_2/V_1)$. Consequently, the total entropy change of the universe is $\Delta S_{\text{universe}} = \Delta S_{\text{sys}} + \Delta S_{\text{surr}} = 0$.
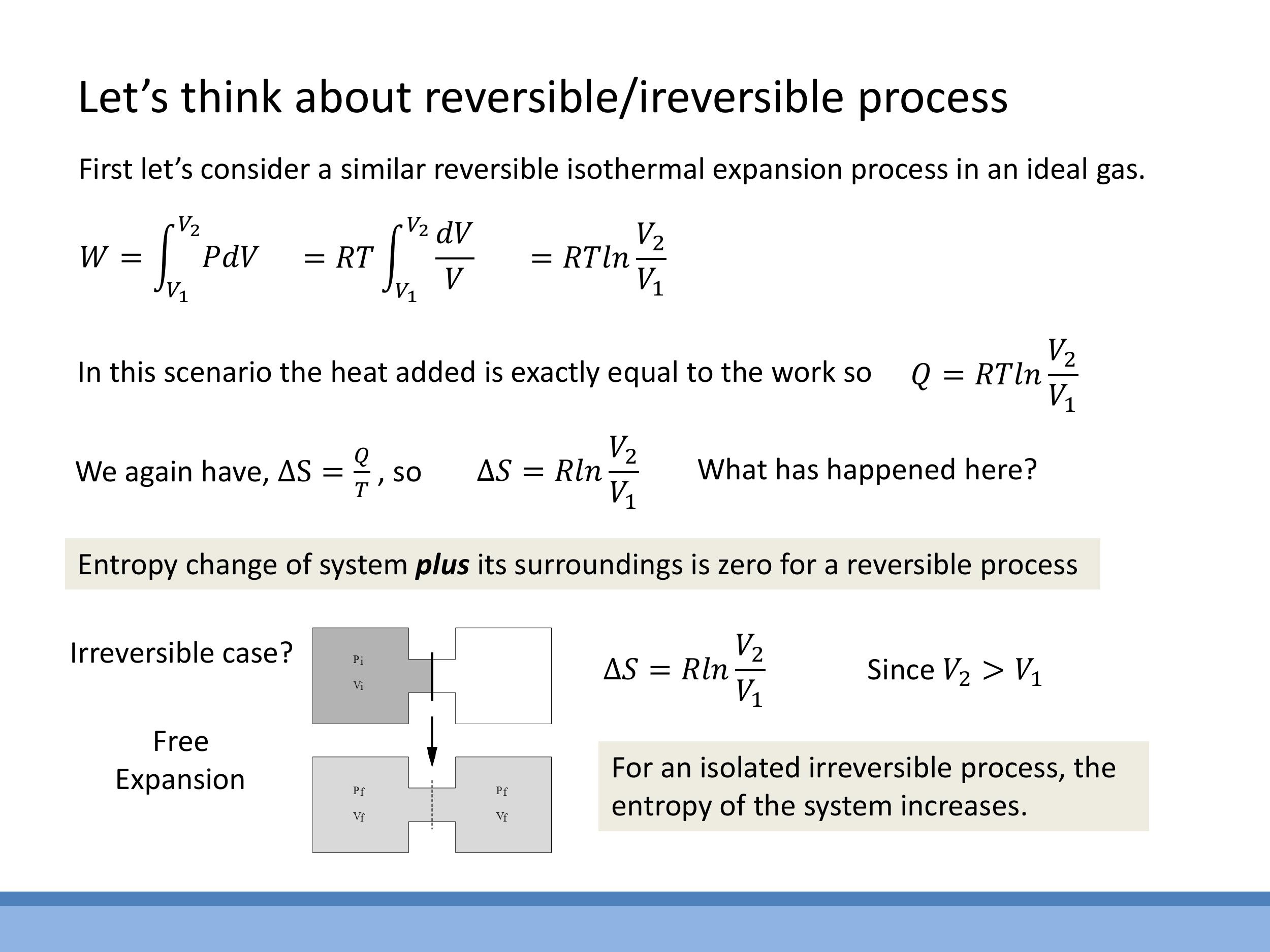
6.3 Irreversible free expansion (isolated)
Consider a gas undergoing a free expansion into a vacuum. This is an irreversible process. Since the gas expands into a vacuum, no external work is done ($W=0$), and if the system is isolated, no heat is transferred ($Q=0$). From the First Law, $\Delta U = Q + W = 0$.
- Even though no heat is exchanged, the gas still moves to a state of higher disorder. Since entropy is a state function, its change depends only on the initial and final states. The final state of a free expansion is the same as that of an isothermal expansion to the same final volume.
- Therefore, the entropy change of the system is $\Delta S_{\text{sys}} = R \ln(V_2/V_1)$.
- The surroundings are unchanged (as it's an isolated process), so $\Delta S_{\text{surr}} = 0$.
- Thus, the total entropy change of the universe is $\Delta S_{\text{universe}} = \Delta S_{\text{sys}} = R \ln(V_2/V_1)$. Since $V_2 > V_1$, this value is positive, confirming that entropy increases for an isolated, irreversible process. This contrasts with the reversible case where $\Delta S_{\text{universe}} = 0$, even though $\Delta S_{\text{sys}}$ might be the same.

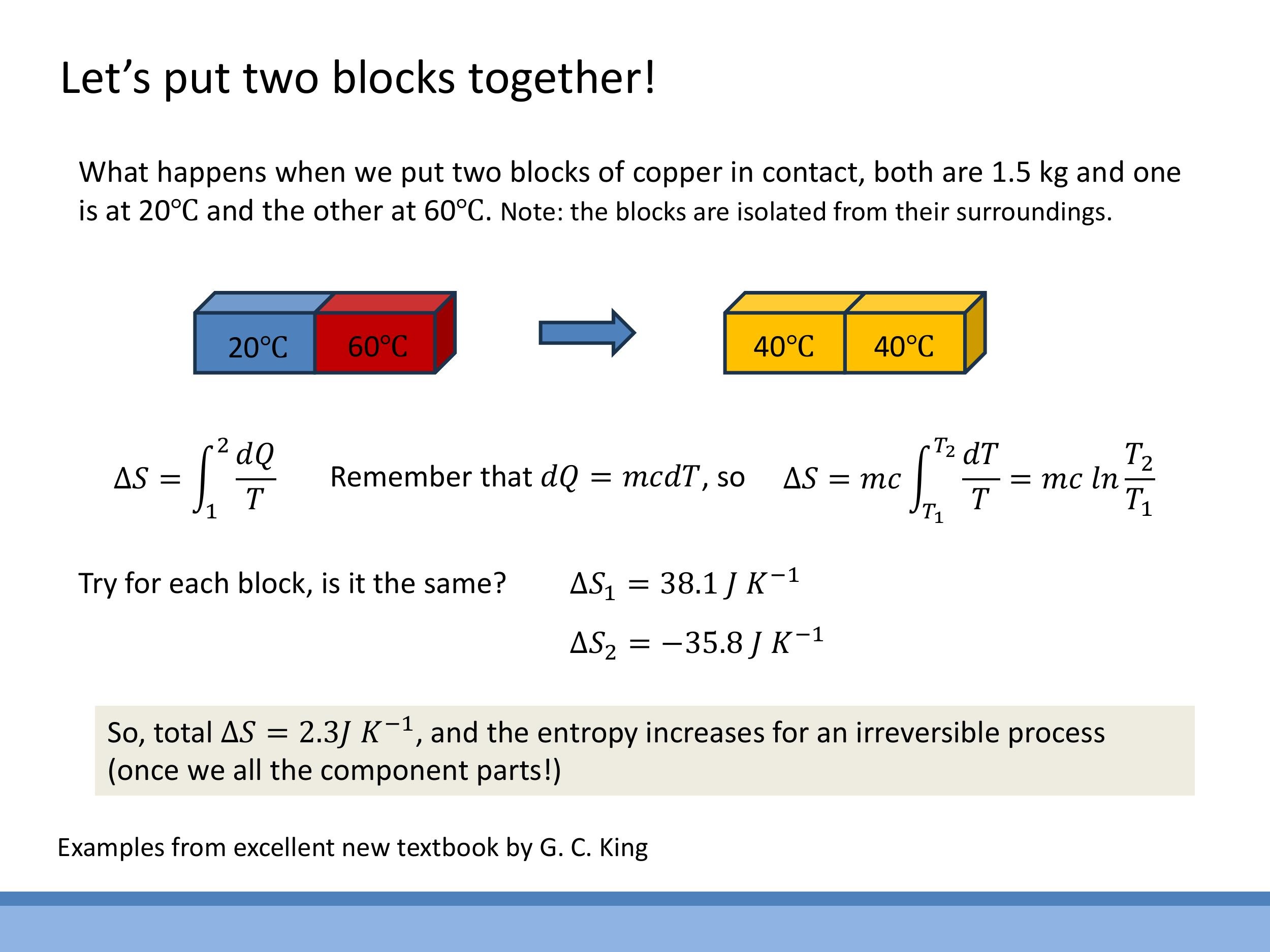
6.4 Two copper blocks reaching equilibrium (isolated, irreversible)
Imagine two $1.5 \, \text{kg} $ copper blocks, one initially at $ 20 \, ^\circ\text{C} $ ($ 293.15 \, \text{K} $) and the other at $ 60 \, ^\circ\text{C} $ ($ 333.15 \, \text{K} $). They are placed in contact within an isolated system and allowed to equilibrate. The final temperature will be $ 40 \, ^\circ\text{C} $ ($ 313.15 \, \text{K}$).
- For each block, the entropy change is calculated using $\Delta S = mc \ln(T_2/T_1)$, where $c$ is the specific heat capacity of copper.
- For the cold block (heating from $20 \, ^\circ\text{C} $ to $ 40 \, ^\circ\text{C} $), $ \Delta S_{\text{cold}} = mc \ln(313.15 \, \text{K}/293.15 \, \text{K}) = +38.1 \, \text{J K}^{-1}$.
- For the hot block (cooling from $60 \, ^\circ\text{C} $ to $ 40 \, ^\circ\text{C} $), $ \Delta S_{\text{hot}} = mc \ln(313.15 \, \text{K}/333.15 \, \text{K}) = -35.8 \, \text{J K}^{-1}$.
- The total entropy change for this isolated, irreversible process is $\Delta S_{\text{total}} = \Delta S_{\text{cold}} + \Delta S_{\text{hot}} = +38.1 \, \text{J K}^{-1} - 35.8 \, \text{J K}^{-1} = +2.3 \, \text{J K}^{-1}$.
This positive total entropy change confirms the irreversibility of the process. The magnitude of the entropy change is greater for the colder body absorbing heat than for the hotter body losing the same amount of heat, due to the $1/T$ factor.
6.5 Heating water in a finite-temperature bath; many small steps reduce $\Delta S$
Consider heating $1 \, \text{kg} $ of water from $ 20 \, ^\circ\text{C} $ ($ 293.15 \, \text{K} $) to $ 80 \, ^\circ\text{C} $ ($ 353.15 \, \text{K} $) by placing it in a large heat bath maintained at a constant $ 80 \, ^\circ\text{C}$.
- For the water (the system), the entropy change is $\Delta S_{\text{water}} = mc \ln(T_2/T_1) = (1 \, \text{kg})(4.2 \times 10^3 \, \text{J kg}^{-1}\text{K}^{-1}) \ln(353.15 \, \text{K}/293.15 \, \text{K}) = +782.4 \, \text{J K}^{-1}$.
- For the heat bath (the surroundings), it loses heat $Q = mc\Delta T = (1 \, \text{kg})(4.2 \times 10^3 \, \text{J kg}^{-1}\text{K}^{-1})(60 \, \text{K}) = 2.52 \times 10^5 \, \text{J} $ at a constant temperature of $ 353.15 \, \text{K} $. So, $ \Delta S_{\text{bath}} = -Q/T_{\text{bath}} = -(2.52 \times 10^5 \, \text{J}) / (353.15 \, \text{K}) = -713.9 \, \text{J K}^{-1}$.
- The total entropy change of the universe is $\Delta S_{\text{universe}} = \Delta S_{\text{water}} + \Delta S_{\text{bath}} = +782.4 \, \text{J K}^{-1} - 713.9 \, \text{J K}^{-1} = +68.5 \, \text{J K}^{-1}$. This positive value indicates an irreversible process.
What if we perform this heating in two steps, first from $20 \, ^\circ\text{C} $ to $ 50 \, ^\circ\text{C} $ (using a $ 50 \, ^\circ\text{C} $ bath), and then from $ 50 \, ^\circ\text{C} $ to $ 80 \, ^\circ\text{C} $ (using an $ 80 \, ^\circ\text{C} $ bath)? If we calculate the total $ \Delta S_{\text{universe}} $ for this multi-step process, it turns out to be $ +35.4 \, \text{J K}^{-1}$, which is smaller than the single-step process. This illustrates a key principle: performing a process in more, smaller, quasi-static steps brings it closer to the ideal reversible limit. In the theoretical limit of an infinite number of infinitesimal steps, the total entropy change of the universe would approach zero.

7) Consolidation: diagnosing processes with entropy
When analysing thermodynamic processes, particularly in problem-solving, it's helpful to have a systematic approach involving entropy. First, identify the type of process (isothermal, adiabatic, isochoric, or isobaric) and determine whether it is reversible or irreversible. Second, always consider both the system and its surroundings, as the total entropy change of the universe ($\Delta S_{\text{universe}}$) dictates the spontaneity and feasibility of the process.
- For a perfectly reversible process, $\Delta S_{\text{universe}} = 0$.
- For an irreversible (spontaneous) process, $\Delta S_{\text{universe}} > 0$.
This framework helps us understand why heat engines cannot be 100% efficient. An engine cycle requires the rejection of heat ($Q_C$) to a cold reservoir at temperature $T_C$. This dumping of heat increases the entropy of the surroundings, providing the necessary positive $\Delta S_{\text{surr}}$ to offset the work extracted and ensure that the total entropy of the universe increases or remains constant, thereby keeping the cycle thermodynamically possible according to the Second Law.
Appendix: Enthalpy and “free” energies (signposts only)
Side Note: This material is supplementary and won't be examined in this course, but it provides useful context for future studies in thermal physics, chemistry, and biology.
These advanced thermodynamic potentials are state functions that are particularly useful for analysing processes under specific constraints, such as constant pressure or constant temperature.
- Enthalpy ($H$): Defined as $H = U + PV$. It is a state function that is especially convenient for processes occurring at constant pressure, where the change in enthalpy ($\Delta H$) directly equals the heat ($Q$) transferred. This links a measurable heat quantity to a state function.
- Helmholtz free energy ($F$ or $A$): This state function encodes the maximum useful work that can be extracted from a system at constant temperature and volume. A negative change in Helmholtz free energy ($\Delta F < 0$) indicates a spontaneous process under these conditions.
- Gibbs free energy ($G$): Defined as $G = H - TS$. This is highly relevant in chemistry and biology, as a negative change in Gibbs free energy ($\Delta G < 0$) indicates a spontaneous reaction or process occurring at constant temperature and pressure.
- Rankine cycle: This is another important thermodynamic cycle, particularly for steam-based power plants. It's an additional example of a heat engine cycle, but its details won't be examined in this course.
These concepts are fundamental in more advanced thermodynamics courses and allow for a deeper understanding of energy transformations and spontaneity in complex systems.



Key takeaways
A heat engine must operate in a cycle, with Carnot's four reversible steps forming the theoretical benchmark. The maximum efficiency for such an engine is $\varepsilon_{\text{Carnot}} = 1 - T_C/T_H$, depending only on the reservoir temperatures.
The Second Law of Thermodynamics is expressed through two equivalent statements: the Kelvin statement, which says no engine can convert all heat from a hot source into work (a cold sink is required), and the Clausius statement, which asserts that heat does not spontaneously flow from cold to hot (work is needed for this).
Entropy ($S$) measures energy dispersal or "quality." Thermodynamically, it's defined as $\mathrm{d}S = \mathrm{d}Q_{\text{rev}}/T$. For any spontaneous (irreversible) process, the total entropy of the universe ($\Delta S_{\text{universe}}$) increases, while for reversible processes, it remains constant ($\Delta S_{\text{universe}} = 0$).
The Carnot cycle, when depicted on a T-S diagram, forms a simple rectangle. This representation clearly shows that heat transfer is the area under the isotherms: $Q_H = T_H \Delta S$ and $Q_C = T_C \Delta S$, which immediately leads to the ratio $Q_C/Q_H = T_C/T_H$.
Calculating entropy changes in various processes provides concrete applications of these principles:
- For a reversible isothermal expansion of an ideal gas, $\Delta S_{\text{sys}} = R \ln(V_2/V_1)$, with the surroundings balancing to yield $\Delta S_{\text{universe}} = 0$.
- For a free expansion (an isolated, irreversible process), $\Delta S_{\text{universe}} = \Delta S_{\text{sys}} = R \ln(V_2/V_1) > 0$.
- When bodies at different temperatures come into thermal contact, the total $\Delta S$ is the sum of individual changes, calculated as $mc \ln(T_2/T_1)$ for each body. The colder body experiences a larger magnitude of entropy change per joule (due to the $1/T$ factor), ensuring $\Delta S_{\text{universe}} > 0$.
- Performing a process in many small, quasi-static steps reduces the total $\Delta S_{\text{universe}}$, demonstrating how such a process approaches the ideal reversible limit.
## Lecture 12: Heat Engines and the Second Law (part 2)
This lecture builds on the concepts of heat engines, cycles on P-V diagrams, reversible and irreversible processes, and adiabats that we discussed previously. Today, we'll formalise the Second Law of Thermodynamics through the Kelvin and Clausius statements. We'll then introduce entropy ($S$) as a crucial new state function, explore T-S diagrams, and learn how to perform practical entropy calculations for simple thermodynamic processes.
Our learning outcomes for this session are to recall the Second Law and understand the equivalence between the Kelvin and Clausius statements. You'll also learn to connect entropy to heat transfer and temperature using the definition $\mathrm{d}S = \mathrm{d}Q_{\text{rev}}/T$. We'll practise transforming a Carnot cycle between P-V and T-S descriptions, and finally, you'll be able to calculate entropy changes in various simple, representative processes, both reversible and irreversible.

### 1) Useful work needs a cycle: the Carnot picture (quick recap)
To perform useful work repeatedly, a working substance must operate in a cycle, meaning it returns to its initial state after each sequence of operations. This cyclical process is typically visualised on a P-V diagram, where the net work done by the system is represented by the area enclosed by the cycle's path.
The Carnot cycle, an idealised and perfectly reversible heat engine, consists of four distinct stages:
1. **Isothermal expansion at $T_H$**: The working substance absorbs heat $Q_H$ from a hot reservoir while expanding at a constant high temperature $T_H$. For an ideal gas undergoing an isothermal process, the change in internal energy $\Delta U$ is zero, so all the absorbed heat is converted into work done by the gas.
2. **Adiabatic expansion**: The system is thermally isolated, meaning no heat is exchanged ($Q=0$). The gas continues to expand, doing work, which causes its temperature to drop from $T_H$ to $T_C$.
3. **Isothermal compression at $T_C$**: The gas is then compressed at a constant low temperature $T_C$, rejecting heat $Q_C$ to a cold reservoir.
4. **Adiabatic compression**: Again, the system is thermally isolated ($Q=0$). Work is done on the gas as it is compressed, increasing its internal energy and raising its temperature back to $T_H$, thus completing the cycle.
From our previous discussion, the efficiency of an ideal Carnot engine is given by $\varepsilon_{\text{Carnot}} = 1 - T_C/T_H$. This formula highlights a fundamental limit: the maximum possible efficiency depends solely on the absolute temperatures of the hot and cold reservoirs, not on the specific working substance. The Stirling cycle, another theoretical ideal engine, replaces the adiabatic legs of the Carnot cycle with isochoric (constant volume) processes but achieves the same maximum efficiency when operating reversibly between the same high and low temperatures, $T_H$ and $T_C$.

### 2) Vocabulary refresh for processes
As we delve deeper into thermodynamics, it's helpful to refresh our understanding of key terms that describe various processes:
* **Isothermal**: A process where the temperature ($T$) of the system remains constant.
* **Isochoric**: A process where the volume ($V$) of the system remains constant.
* **Isobaric**: A process where the pressure ($P$) of the system remains constant.
* **Isentropic**: A process where the entropy ($S$) of the system remains constant. This usually implies a reversible adiabatic process.
* **Adiabatic**: A process where no heat ($Q$) is transferred into or out of the system ($\mathrm{d}Q = 0$).
These definitions are crucial for interpreting thermodynamic diagrams and calculations.
### 3) The Second Law: Kelvin and Clausius statements and why they’re equivalent
The Second Law of Thermodynamics places fundamental limitations on how energy can be converted and transferred. It has two equivalent formulations, known as the Kelvin (or Kelvin-Planck) statement and the Clausius statement.
The **Kelvin statement** asserts that it is impossible for any cyclic device to extract heat from a single hot reservoir and convert it entirely into useful work. This means that a cold sink, or a cold reservoir, is always necessary for a heat engine to operate continuously and produce net work. Without a cold sink to dump excess heat, the cycle cannot be completed without violating the Second Law.
The **Clausius statement** declares that heat does not spontaneously flow from a colder body to a hotter body. This aligns with our everyday experience: a hot cup of coffee cools down in a room, but a cold drink doesn't spontaneously get hotter by absorbing heat from the cooler room. To move heat "uphill," from a cold region to a hot region (as in a refrigerator or heat pump), external work must be supplied to the system.
These two statements are not independent; they are two sides of the same fundamental law. If one statement were false, it would be possible to construct a hypothetical device that violates the other. For instance, if the Kelvin statement were false, we could build an engine that converts all heat into work. We could then use some of that work to drive a refrigerator (which is a device that moves heat from cold to hot) in such a way that it violates the Clausius statement. Similarly, if the Clausius statement were false, we could create a device that spontaneously moves heat from cold to hot, and by combining it with an engine, we could violate the Kelvin statement. Thus, their equivalence means that if one is true, the other must also be true, and vice-versa.


### 4) Entropy $S$: what it measures and its definitions
Entropy ($S$) is a central concept in thermodynamics, providing a quantitative measure of the "disorder" or "energy spread" within a system. We can think of its physical meaning in several ways:
* **Disorder view**: This is the most common intuitive picture. A gas, with its randomly moving molecules, has higher entropy than a liquid, which in turn has higher entropy than an ordered crystalline solid. The more disordered a system, the higher its entropy.
* **Energy spread view**: Entropy can also be understood as a measure of how widely energy is distributed among the accessible microscopic states of a system. In a gas, energy is spread over a vast range of positions and velocities for its molecules, leading to high entropy. In contrast, in a solid, energy is mostly confined to vibrations around fixed positions, resulting in lower entropy.
* **Energy quality view**: Entropy is inversely related to the "quality" or usability of energy. High-quality, concentrated energy (like sunlight) is considered low-entropy, while dispersed, "waste heat" is high-entropy. Biological processes, for example, increase the entropy of the universe by degrading high-quality energy into more dispersed, lower-quality forms.
The **thermodynamic definition** of entropy provides a precise mathematical formulation. It states that an infinitesimal change in entropy ($\mathrm{d}S$) is equal to the infinitesimal amount of heat transferred reversibly ($\mathrm{d}Q_{\text{rev}}$) divided by the absolute temperature ($T$) at which the transfer occurs:
$$\mathrm{d}S = \frac{\mathrm{d}Q_{\text{rev}}}{T}$$
The $1/T$ factor in this definition is crucial. To build intuition, consider Peter Atkins' analogy: the same "sneeze" (representing an amount of heat $\mathrm{d}Q$) causes a much larger disturbance (a larger $\mathrm{d}S$) in a quiet library (low $T$) than on a bustling street (high $T$). This helps us understand why a given amount of heat has a more significant disordering effect on a colder system.
*Side Note:* The **statistical definition** of entropy, formulated by Ludwig Boltzmann, connects entropy to the microscopic world. His famous equation, $S = k \ln W$, relates entropy ($S$) to Boltzmann's constant ($k$) and the natural logarithm of the number of accessible microstates ($W$) for a system. While this provides a deeper understanding of entropy's statistical nature, we won't use it for calculations in this course.

### 5) The Carnot cycle on a T-S diagram and a simpler route to $\varepsilon$
While P-V diagrams are useful for visualising work, Temperature-Entropy (T-S) diagrams offer a powerful alternative, especially for understanding the Carnot cycle and its efficiency.
On a T-S diagram, the four reversible stages of the Carnot cycle transform into a simple rectangle:
* **Isothermal expansion (a→b)**: During this stage, the temperature remains constant at $T_H$, and the entropy of the system increases as the gas expands. This is represented by a horizontal line segment moving from left to right on the T-S diagram.
* **Adiabatic expansion (b→c)**: This is a reversible process with no heat transfer ($\mathrm{d}Q = 0$). Since $\mathrm{d}S = \mathrm{d}Q_{\text{rev}}/T$, the entropy change is zero. As the gas expands, its temperature drops from $T_H$ to $T_C$. This is represented by a vertical line segment moving downwards.
* **Isothermal compression (c→d)**: The temperature remains constant at $T_C$, and the entropy of the system decreases as the gas is compressed. This is a horizontal line segment moving from right to left.
* **Adiabatic compression (d→a)**: Again, there is no heat transfer, so the entropy change is zero. Work is done on the gas, raising its temperature back to $T_H$, completing the cycle with a vertical line segment moving upwards.
The resulting shape on a T-S diagram is a perfect rectangle bounded by the hot temperature $T_H$, the cold temperature $T_C$, and the entropy values $S_1$ and $S_2$.
This T-S representation provides a remarkably straightforward way to derive the Carnot efficiency. On a T-S diagram, the heat transferred during an isothermal process is simply the area under the horizontal line representing that isotherm.
* The heat absorbed from the hot reservoir ($Q_H$) is the area under the top isotherm: $Q_H = T_H \Delta S$, where $\Delta S = S_2 - S_1$.
* The heat rejected to the cold reservoir ($Q_C$) is the area under the bottom isotherm: $Q_C = T_C \Delta S$, where $\Delta S = S_2 - S_1$.
By taking the ratio of these heats, we immediately find $Q_C/Q_H = T_C/T_H$. Substituting this into the general efficiency formula, $\varepsilon = 1 - Q_C/Q_H$, yields the Carnot efficiency: $\varepsilon = 1 - T_C/T_H$. This demonstrates that both the P-V and T-S diagrams describe the same underlying physics, but the T-S diagram offers a more elegant and immediate route to understanding the efficiency, compressing the algebra into simple geometry.

### 6) Calculating entropy changes: representative worked cases
Entropy is a state function, meaning its change depends only on the initial and final states of a system, not on the path taken. However, when calculating $\Delta S$, we often need to consider a reversible path between those states. Let's look at some examples.
#### 6.1 Reversible phase change at fixed T: melting ice at 0 °C
Consider a small amount of ice melting into water at $0\,^\circ\text{C}$ ($273.15\,\text{K}$). This is an idealised reversible process.
* For the ice, which absorbs heat (latent heat of fusion, $L_{\text{fus}}$), the entropy change is $\Delta S_{\text{ice}} = Q/T = mL_{\text{fus}}/T$. If we take $m = 15\,\text{g}$ ($0.015\,\text{kg}$) and $L_{\text{fus}} = 334\,\text{kJ kg}^{-1}$, then $\Delta S_{\text{ice}} = (0.015\,\text{kg})(334 \times 10^3\,\text{J kg}^{-1}) / (273.15\,\text{K}) \approx +18.3\,\text{J K}^{-1}$.
* The water (or surroundings) provides this heat, so its entropy change is equal in magnitude but opposite in sign: $\Delta S_{\text{water}} = -18.3\,\text{J K}^{-1}$.
* For the total isolated and reversible system, the total entropy change is $\Delta S_{\text{total}} = \Delta S_{\text{ice}} + \Delta S_{\text{water}} = 0$. This is an isentropic process. The equal and opposite entropy changes reflect the reversible heat exchange at a fixed temperature.

#### 6.2 Reversible isothermal expansion of an ideal gas
For a reversible isothermal expansion of an ideal gas, the internal energy change $\Delta U = 0$. Therefore, the heat absorbed ($Q$) is equal to the work done by the gas ($W$). The work done during an isothermal expansion of one mole of an ideal gas is $W = \int P\,\mathrm{d}V = RT \ln(V_2/V_1)$.
* Since $Q = W$, the heat absorbed is $Q = RT \ln(V_2/V_1)$.
* The entropy change of the system is $\Delta S_{\text{sys}} = Q/T = R \ln(V_2/V_1)$. Since $V_2 > V_1$, the system's entropy increases.
* For a fully reversible process, the surroundings must experience an equal and opposite entropy change, so $\Delta S_{\text{surr}} = -R \ln(V_2/V_1)$. Consequently, the total entropy change of the universe is $\Delta S_{\text{universe}} = \Delta S_{\text{sys}} + \Delta S_{\text{surr}} = 0$.

#### 6.3 Irreversible free expansion (isolated)
Consider a gas undergoing a free expansion into a vacuum. This is an irreversible process. Since the gas expands into a vacuum, no external work is done ($W=0$), and if the system is isolated, no heat is transferred ($Q=0$). From the First Law, $\Delta U = Q + W = 0$.
* Even though no heat is exchanged, the gas still moves to a state of higher disorder. Since entropy is a state function, its change depends only on the initial and final states. The final state of a free expansion is the same as that of an isothermal expansion to the same final volume.
* Therefore, the entropy change of the system is $\Delta S_{\text{sys}} = R \ln(V_2/V_1)$.
* The surroundings are unchanged (as it's an isolated process), so $\Delta S_{\text{surr}} = 0$.
* Thus, the total entropy change of the universe is $\Delta S_{\text{universe}} = \Delta S_{\text{sys}} = R \ln(V_2/V_1)$. Since $V_2 > V_1$, this value is positive, confirming that entropy increases for an isolated, irreversible process. This contrasts with the reversible case where $\Delta S_{\text{universe}} = 0$, even though $\Delta S_{\text{sys}}$ might be the same.

#### 6.4 Two copper blocks reaching equilibrium (isolated, irreversible)
Imagine two $1.5\,\text{kg}$ copper blocks, one initially at $20\,^\circ\text{C}$ ($293.15\,\text{K}$) and the other at $60\,^\circ\text{C}$ ($333.15\,\text{K}$). They are placed in contact within an isolated system and allowed to equilibrate. The final temperature will be $40\,^\circ\text{C}$ ($313.15\,\text{K}$).
* For each block, the entropy change is calculated using $\Delta S = mc \ln(T_2/T_1)$, where $c$ is the specific heat capacity of copper.
* For the cold block (heating from $20\,^\circ\text{C}$ to $40\,^\circ\text{C}$), $\Delta S_{\text{cold}} = mc \ln(313.15\,\text{K}/293.15\,\text{K}) = +38.1\,\text{J K}^{-1}$.
* For the hot block (cooling from $60\,^\circ\text{C}$ to $40\,^\circ\text{C}$), $\Delta S_{\text{hot}} = mc \ln(313.15\,\text{K}/333.15\,\text{K}) = -35.8\,\text{J K}^{-1}$.
* The total entropy change for this isolated, irreversible process is $\Delta S_{\text{total}} = \Delta S_{\text{cold}} + \Delta S_{\text{hot}} = +38.1\,\text{J K}^{-1} - 35.8\,\text{J K}^{-1} = +2.3\,\text{J K}^{-1}$.
This positive total entropy change confirms the irreversibility of the process. The magnitude of the entropy change is greater for the colder body absorbing heat than for the hotter body losing the same amount of heat, due to the $1/T$ factor.

#### 6.5 Heating water in a finite-temperature bath; many small steps reduce $\Delta S$
Consider heating $1\,\text{kg}$ of water from $20\,^\circ\text{C}$ ($293.15\,\text{K}$) to $80\,^\circ\text{C}$ ($353.15\,\text{K}$) by placing it in a large heat bath maintained at a constant $80\,^\circ\text{C}$.
* For the water (the system), the entropy change is $\Delta S_{\text{water}} = mc \ln(T_2/T_1) = (1\,\text{kg})(4.2 \times 10^3\,\text{J kg}^{-1}\text{K}^{-1}) \ln(353.15\,\text{K}/293.15\,\text{K}) = +782.4\,\text{J K}^{-1}$.
* For the heat bath (the surroundings), it loses heat $Q = mc\Delta T = (1\,\text{kg})(4.2 \times 10^3\,\text{J kg}^{-1}\text{K}^{-1})(60\,\text{K}) = 2.52 \times 10^5\,\text{J}$ at a constant temperature of $353.15\,\text{K}$. So, $\Delta S_{\text{bath}} = -Q/T_{\text{bath}} = -(2.52 \times 10^5\,\text{J}) / (353.15\,\text{K}) = -713.9\,\text{J K}^{-1}$.
* The total entropy change of the universe is $\Delta S_{\text{universe}} = \Delta S_{\text{water}} + \Delta S_{\text{bath}} = +782.4\,\text{J K}^{-1} - 713.9\,\text{J K}^{-1} = +68.5\,\text{J K}^{-1}$. This positive value indicates an irreversible process.
What if we perform this heating in two steps, first from $20\,^\circ\text{C}$ to $50\,^\circ\text{C}$ (using a $50\,^\circ\text{C}$ bath), and then from $50\,^\circ\text{C}$ to $80\,^\circ\text{C}$ (using an $80\,^\circ\text{C}$ bath)? If we calculate the total $\Delta S_{\text{universe}}$ for this multi-step process, it turns out to be $+35.4\,\text{J K}^{-1}$, which is smaller than the single-step process. This illustrates a key principle: performing a process in more, smaller, quasi-static steps brings it closer to the ideal reversible limit. In the theoretical limit of an infinite number of infinitesimal steps, the total entropy change of the universe would approach zero.

### 7) Consolidation: diagnosing processes with entropy
When analysing thermodynamic processes, particularly in problem-solving, it's helpful to have a systematic approach involving entropy. First, identify the type of process (isothermal, adiabatic, isochoric, or isobaric) and determine whether it is reversible or irreversible. Second, always consider both the system and its surroundings, as the total entropy change of the universe ($\Delta S_{\text{universe}}$) dictates the spontaneity and feasibility of the process.
* For a perfectly **reversible process**, $\Delta S_{\text{universe}} = 0$.
* For an **irreversible (spontaneous) process**, $\Delta S_{\text{universe}} > 0$.
This framework helps us understand why heat engines cannot be 100% efficient. An engine cycle requires the rejection of heat ($Q_C$) to a cold reservoir at temperature $T_C$. This dumping of heat increases the entropy of the surroundings, providing the necessary positive $\Delta S_{\text{surr}}$ to offset the work extracted and ensure that the total entropy of the universe increases or remains constant, thereby keeping the cycle thermodynamically possible according to the Second Law.
## Appendix: Enthalpy and “free” energies (signposts only)
*Side Note:* This material is supplementary and won't be examined in this course, but it provides useful context for future studies in thermal physics, chemistry, and biology.
These advanced thermodynamic potentials are state functions that are particularly useful for analysing processes under specific constraints, such as constant pressure or constant temperature.
* **Enthalpy ($H$)**: Defined as $H = U + PV$. It is a state function that is especially convenient for processes occurring at constant pressure, where the change in enthalpy ($\Delta H$) directly equals the heat ($Q$) transferred. This links a measurable heat quantity to a state function.
* **Helmholtz free energy ($F$ or $A$)**: This state function encodes the maximum useful work that can be extracted from a system at constant temperature and volume. A negative change in Helmholtz free energy ($\Delta F < 0$) indicates a spontaneous process under these conditions.
* **Gibbs free energy ($G$)**: Defined as $G = H - TS$. This is highly relevant in chemistry and biology, as a negative change in Gibbs free energy ($\Delta G < 0$) indicates a spontaneous reaction or process occurring at constant temperature and pressure.
* **Rankine cycle**: This is another important thermodynamic cycle, particularly for steam-based power plants. It's an additional example of a heat engine cycle, but its details won't be examined in this course.
These concepts are fundamental in more advanced thermodynamics courses and allow for a deeper understanding of energy transformations and spontaneity in complex systems.




## Key takeaways
A heat engine must operate in a cycle, with Carnot's four reversible steps forming the theoretical benchmark. The maximum efficiency for such an engine is $\varepsilon_{\text{Carnot}} = 1 - T_C/T_H$, depending only on the reservoir temperatures.
The Second Law of Thermodynamics is expressed through two equivalent statements: the Kelvin statement, which says no engine can convert all heat from a hot source into work (a cold sink is required), and the Clausius statement, which asserts that heat does not spontaneously flow from cold to hot (work is needed for this).
Entropy ($S$) measures energy dispersal or "quality." Thermodynamically, it's defined as $\mathrm{d}S = \mathrm{d}Q_{\text{rev}}/T$. For any spontaneous (irreversible) process, the total entropy of the universe ($\Delta S_{\text{universe}}$) increases, while for reversible processes, it remains constant ($\Delta S_{\text{universe}} = 0$).
The Carnot cycle, when depicted on a T-S diagram, forms a simple rectangle. This representation clearly shows that heat transfer is the area under the isotherms: $Q_H = T_H \Delta S$ and $Q_C = T_C \Delta S$, which immediately leads to the ratio $Q_C/Q_H = T_C/T_H$.
Calculating entropy changes in various processes provides concrete applications of these principles:
* For a reversible isothermal expansion of an ideal gas, $\Delta S_{\text{sys}} = R \ln(V_2/V_1)$, with the surroundings balancing to yield $\Delta S_{\text{universe}} = 0$.
* For a free expansion (an isolated, irreversible process), $\Delta S_{\text{universe}} = \Delta S_{\text{sys}} = R \ln(V_2/V_1) > 0$.
* When bodies at different temperatures come into thermal contact, the total $\Delta S$ is the sum of individual changes, calculated as $mc \ln(T_2/T_1)$ for each body. The colder body experiences a larger magnitude of entropy change per joule (due to the $1/T$ factor), ensuring $\Delta S_{\text{universe}} > 0$.
* Performing a process in many small, quasi-static steps reduces the total $\Delta S_{\text{universe}}$, demonstrating how such a process approaches the ideal reversible limit.














